unscientific
- 1,728
- 13
Homework Statement
Simple proof on why ∇∅ is normal to surface of ∅(x,y,z) = constant
Homework Equations
The Attempt at a Solution
Last edited:
unscientific said:Homework Statement
Simple proof on why ∇∅ is normal to surface of ∅(x,y,z) = constant
Homework Equations
The Attempt at a Solution
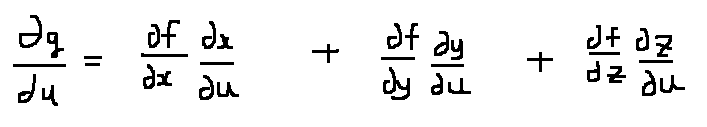
Dick said:The 'attempt at a proof' is a good 'relevant equation' maybe with a little fixing. Now what's the attempt at a proof?
unscientific said:Sorry, I attached the wrong picture!
Dick said:Ok that's more like it. Now if you want to make the string of equations function as a proof you need to add some words explaining why it's a proof. What kind of a curve are you taking ##\vec s## to be? And why does the last line show grad(phi) is normal to the surface?
unscientific said:s is the distance along the curve, t is the unit tangent vector to the curve...
does this proof make sense?
Dick said:Same thing I said before. A proper proof involves at least a little narrative in words as to what things are, like you just did, and how the final equation justifies the conclusion that grad(phi) is normal to the level surface of phi. Supply those and it will work fine.
unscientific said:Thanks! I will do that in future. The math is correct, right?