VinnyCee
- 486
- 0
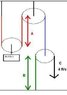
The cable at C is being pulled down at a velocity of 4 \frac{ft}{s}. The cable at C is also decelerating at a rate of 2 \frac{ft}{s^2}. At what velocity and acceleration is the block at A moving?
http://img222.imageshack.us/img222/729/engr204problem121795wl.jpg
I have the following equations for the problem worked out:
\ell\,=\,2\,S_A\,+\,\left(h\,-\,S_B\right)
\frac{d}{dt}\,\left[\ell\,=\,2\,S_A\,+\,\left(h\,-\,S_B\right)\right]
0\,=\,2\,V_A\,-\,V_B
V_A\,=\,-\frac{V_C}{2}
V_A\,=\,-\frac{-4}{2}\,=\,2\,\frac{ft}{s}
This answer is NOT correct, it is off by a factor of two. Can anyone tell why?
http://img222.imageshack.us/img222/729/engr204problem121795wl.jpg
I have the following equations for the problem worked out:
\ell\,=\,2\,S_A\,+\,\left(h\,-\,S_B\right)
\frac{d}{dt}\,\left[\ell\,=\,2\,S_A\,+\,\left(h\,-\,S_B\right)\right]
0\,=\,2\,V_A\,-\,V_B
V_A\,=\,-\frac{V_C}{2}
V_A\,=\,-\frac{-4}{2}\,=\,2\,\frac{ft}{s}
This answer is NOT correct, it is off by a factor of two. Can anyone tell why?
Attachments
Last edited by a moderator: