Pulley problem with moment of inetia

AI Thread Summary
The discussion centers on calculating the acceleration of block A, which is influenced by the mass of block B and the moment of inertia of the pulley. The pulley, modeled as a thin disk with mass, introduces resistance to the system's acceleration due to its rotational inertia. Understanding the relationship between angular and linear acceleration is crucial, as the pulley’s mass affects the overall dynamics. The moment of inertia plays a key role in this scenario, as it impacts the acceleration experienced by block A. This problem highlights the complexities of incorporating rotational dynamics in systems with pulleys.
Iansno1
Messages
2
Reaction score
0
Problem

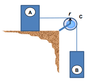
As shown below, Block A has mass 'M' and rests on a surface with a coefficient of kinetic friction 'Uk' .The cord attached to A passes over a pulley at C and is attached to a block B of mass '2M'. If B is released calculate the acceleration of A.

Assume the cord does not slip over the pulley. The Pulley can be approximated as a thin disk of radius 'r' and mass 'M/4' . Neglect the mass of the cord
Relevant equations

moment of inertia of the disk: I=0.5*M*r2
Not sure where to start
 

Attachments

  • Capture.PNG
    Capture.PNG
    4.7 KB · Views: 433
Physics news on Phys.org
with free body diagrams?

ehild
 
How does the Moment of inertia come into the equation? I can do these problems when the pulley is assumed to have no mass and no friction.
 
Iansno1 said:
How does the Moment of inertia come into the equation? I can do these problems when the pulley is assumed to have no mass and no friction.

Moment of inertia is the analog of mass for rotational motion. The moment of inertia resists angular acceleration in the same fashion as mass resists linear acceleration.

In this problem the pulley adds resistance to the acceleration of the overall system because the cord does not slip, and so must cause angular acceleration of the pulley. The angular acceleration is related to the linear acceleration (how?).
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Mass and pulley system (Rotational Dynamics)
Replies
9
Views
2K
Ideal Vs Real Mass Pulley system
Replies
10
Views
5K
How Do You Calculate the Angular Motion of a Pulley System?
Replies
15
Views
2K
Moment of Inertia with pulley and two masses on a string (iWTSE.org)
Replies
8
Views
12K
Newton's Second Law (Pulley Sustem)
Replies
3
Views
2K
Pulley's mass is invariant to the physics problem?
Replies
13
Views
1K
Problem with pulleys - two fixed and one movable
Replies
22
Views
323
Friction problem involving a pulley
Replies
10
Views
3K
Experimental Design: Pulley and Mass Hangers
Replies
30
Views
3K
System of two pulleys and three masses
Replies
22
Views
6K

Hot Threads

Recent Insights

Back
Top