Lamoid
- 44
- 0
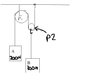
The weights of the objects are 200 N and 300 N. The pulleys are essentially frictionless and massless. P1 has a stationary axle but P2 is free to move up and down. Find the tensions FT1 and FT2 and the acceleration of each body.
Diagram I made in paint attached.
Now my problem is not that I can't get the right answer but that I don't understand why. It gives me a hint that the acceleration of block B is half (and in the opposite direction of course) that of block A and I cannot not figure out why that is. Can anyone explain it to me?
And yes, the diagram sucks but the A block is moving down, B is moving up.
Diagram I made in paint attached.
Now my problem is not that I can't get the right answer but that I don't understand why. It gives me a hint that the acceleration of block B is half (and in the opposite direction of course) that of block A and I cannot not figure out why that is. Can anyone explain it to me?
And yes, the diagram sucks but the A block is moving down, B is moving up.