Analyzing Tensions in a Mass-Weight System

  • Thread starter Thread starter aatari
  • Start date Start date
  • Tags Tags
    Homework Review
AI Thread Summary
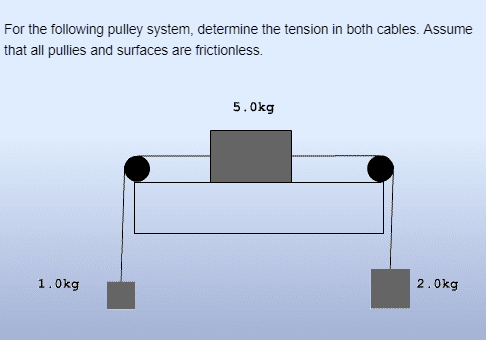
The discussion focuses on a student's solution regarding tensions in a mass-weight system, which lacks clarity in notation and definitions of forces. Reviewers express confusion over the repeated notation "FT=FT=FT" and suggest that it does not effectively convey the calculations. They note that the calculation for the 5kg mass indicates no vertical acceleration, which is assumed to be correct without proof. Additionally, the calculations for the 1kg and 2kg masses are acknowledged as acceptable, but the use of distinct symbols for different tensions is recommended. Overall, the feedback emphasizes the need for clearer notation and definitions to enhance understanding.
aatari
Messages
73
Reaction score
3
Hi guys, could someone please have a look at my solution and let me know if it makes any sense.

Homework Statement


Capture.PNG


Homework Equations


N/A

The Attempt at a Solution


ans.PNG
[/B]
 
Physics news on Phys.org
I don't understand your notation. Can you please define what the various forces represent. And what does FT=FT=FT mean?
 
Your "For 5kg" calculation appears to be showing that the mass on the table has no vertical acceleration. I think we can assume that without proof.
Your "For 1kg" and "For 2kg" calculations are ok except that you should use different symbols for the two different tensions.
As Chet notes, "FT=FT=FT" is not very illuminating, and I can make no sense of the calculation which follows.
 

Thread 'Struggling to understand the concept of this question (ice cube in water optics question)'

TL;DR Summary: I came across this question from a Sri Lankan A-level textbook. Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water. I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
View full post »
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Why are the forces on torque tension and not the weight of the mass?
Replies
7
Views
1K
Find the Magnitude of Average velocity using the given vectors
Replies
2
Views
997
Acceleration and Tension in a Two-Block System on an Inclined Plane
Replies
8
Views
2K
Motion of a system that has two masses and three pulleys
Replies
11
Views
2K
Tension in the wire connecting two blocks
Replies
5
Views
2K
with this tension problem -- Mass on an accelerating cable
Replies
3
Views
2K
Calculating Tension in a Telephone Wire with Mass and Angle
Replies
5
Views
3K
Problem with pulleys - two fixed and one movable
Replies
22
Views
374
Solve Tension in Rope: 110 Kg Anvil & 9.81m/s^2 Force
Replies
13
Views
2K
Tension in Suspended Traffic Light Problem
Replies
4
Views
4K

Hot Threads

Recent Insights

Back
Top