Pulleys and Conservation of Energy

[zx95]

1. In the system shown in the figure, the pulleys on the left and right are fixed, but the pulley in the center can move left or right. The two hanging masses are identical, and the pulleys and ropes are all massless. Find the upward acceleration of the mass on the left, in terms of g.
2. I have to solve this problem using only Conservation of Energy. The following equations are relevant: K = (1/2)mv^2 and U = mgy

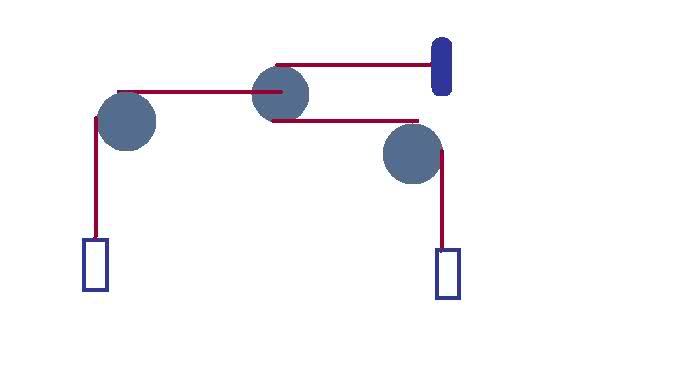
3. I began by setting up a general Conservation of Energy equation.

I'm calling the left mass m1 and the right mass m2
m1 = m2 = m

ΔU1 + ΔU2 + ΔK2 = ΔK1
mgΔy1 + mgΔy2 + (1/2)mv2^2 = (1/2)m1^2

(( v^2 = 2aΔy)) Substitute kinematic equation for velocity

gΔy1 + gΔy2 + aΔy2 = aΔy1

(( Δy1 = -2Δy2)) Substitute Δy1 in terms of Δy2

-2gΔy2 + gΔy2 + aΔy2 = -2aΔy2
-2g + g = -2a - a
-g = -3a
(1/3)g = a

This however, doesn't seem to be correct. Any hints on where I may have gone wrong? Thanks!

 

[PhanthomJay]

Looking at this quickly, a couple of points:
(1) the acceleration of the masses, and hence their speeds, are not the same; one of them accelerates at twice the rate of the other.
(2) Your conservation of energy equation is wrong. It's delta K_total plus delta U_total =0. I'm not sure why you have one of the delta K's on the other side of the equation.