AlonsoDeMaria
- 5
- 0
1. Homework Statement
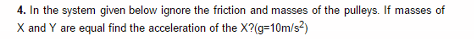

2. Homework Equations
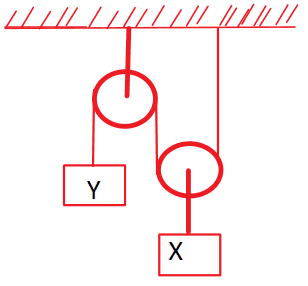
How to get ax=2ay?
3. The Attempt at a Solution
a=10m/s2
And the solution I found was a=2m/s2
I found this at : http://www.physicstutorials.org/home/exams/dynamics-exams/142-dynamics-exam1
2. Homework Equations
How to get ax=2ay?
3. The Attempt at a Solution
a=10m/s2
And the solution I found was a=2m/s2
I found this at : http://www.physicstutorials.org/home/exams/dynamics-exams/142-dynamics-exam1
Attachments
Last edited: