I'm really disappointed with this discussion. So many voices, none contributing anything useful. This forum should be by physicists who know math.
What we have is a curvature of a cycloid, a purely mathematical problem. Here is how to deal with it.
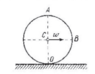
To begin, pick a frame of reference. The geometry is purely 2-dimensional and we need only x and y coordinates.
I choose the origin at the centre of the cylinder and the x-direction along the direction of the movement of the cylinder.
Let me denote the position of the axis of the cylinder as u and the radius of the cylinder as R. Since the cylinder rotates, the angle of the cylinder (measured from its starting position) will be u/R.
Therefore, the coordinates of the point A (top of the cylinder) will be (u+R sin(u/R), R cos(u/R)). The coordinates of the point B will be (u +R cos(u/R), -R sin(u/R)).
Now, we have x, and y coordinates of the points, It is time to apply the curvature formula as given in my previous post (see the link
https://en.wikipedia.org/wiki/Curvature#Precise_definition)
For the point A, the X-coordinate is u + R sin(u/R), therefore, the derivative (with respect to u) is x' = 1 + cos(u/R) and the second derivative x" = - sin(u/R)/R.
Similarity, the Y-coordinate y = R cos(u/R) can be differentiated to give y' = - sin(u/R) and y" = - cos(u/R)/R.
Now, all we have to do is to substitute the above expression into the formula for the curvature. Denoting the radius of the curvature as r (lower case) we have
## \frac 1 r = \kappa = \frac {[ x'y"-y'x"]}{(x' ^2 + y'^2)^{3/2}} ##.
At this point I could substitute the expression for the first and second derivatives into the above formula, then see the value of u to 0 and evaluate. This would be too complex, I will set u = 0, evaluate the derivatives and substitute the values into the expression for the curvature.
Here we go, if I set u = u, x' = 2, x" =0, y' =0, y" = -1/R, therefore, the curvature is
## \frac 1 r = \kappa = \frac {[ 2(-1/R) - 0*0]}{(2^2 + 0^2)^{3/2}} = \frac 1 {4R} ##
Therefore, the radius of curvature of the point A is 4 times the radius of the cylinder !.
Similar calculations can be done for the point B.