Rank the rate of speed changing of object?

[isukatphysics69]

Homework Statement

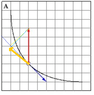
Rank the rate at which the speed of each object is changing, greatest first. Ignore the sign; rank the magnitude or absolute value only.

Homework Equations

The red vector is the acceleration[/B]

The Attempt at a Solution

I have A>F>D>E=C and the program is telling me i am wrong. I am square rooting the sum of the squares of the components of the red vectors. I have A=4,F=SQRT(10),D=SQRT(8), C AND D = SQRT(5).

 

[isukatphysics69]

OK I THINK I KNOW WHAT I AM DOING WRONG. I NEED TO FIND THE PARRALEL COMPONENT NOT LOOK AT THE ACCELERATION VECTOR!

 

[isukatphysics69]

Ok, now i have D>A>F>E>C after using Aparrellel = Acosine(theta) and it is still saying i am wrong after getting the values A=2,C=0,D=2.82,E=0.388,F=1.5. I estimated the angles between velocity and acceleration vectors

 

[ehild]

OK I THINK I KNOW WHAT I AM DOING WRONG. I NEED TO FIND THE PARRALEL COMPONENT NOT LOOK AT THE ACCELERATION VECTOR!

Parallel component of what? Parallel with what?

 

[isukatphysics69]

Parallel component of what? Parallel with what?

Ok hi, i need to find the parrelel component of the acceleration vector (the red one in the picture)

 

[ehild]

Ok hi, i need to find the parrelel component of the acceleration vector (the red one in the picture)

Parallel with what?
You can read the components of the velocity and acceleration vectors, and calculate the scalar products, instead of estimating the angles.

 

[isukatphysics69]

Parallel component of what? Parallel with what?

So i have to rank the rate that the speed of the particle is changing which means i have to find the acceleration parrelel component of the acceleration vector i believe. so i used the formula that my professor said and it is acos(theta) and i estimated the thetas. i have the values A=2 C=0 D=2.8 E=0.38 F=1.5

 

[isukatphysics69]

Parallel with what?

The acceleration vector is parrelel with the velocity vector

 

[isukatphysics69]

Parallel with what?
You can read the components of the velocity and acceleration vectors, and calculate the scalar products, instead of estimating the angles.

Dot product?

 

[ehild]

The acceleration vector is parrelel with the velocity vector

You mean the component of the acceleration vector, parallel with the velocity vector.

 

[ehild]

Dot product?

Yes. Dot product of the acceleration with the unit vector in the direction of the velocity.

 

[isukatphysics69]

Yes.

Yes. Dot product of the acceleration with the unit vector in the direction of the velocity.

Using the dot product i have A>F>E>C=D A=6, F=5, E=2, C and E =0

 

[isukatphysics69]

Program is telling me i am incorrect. >=[
So we start at the particles position and have wherever the velocity vector is pointing as the positive direction right?

 

[ehild]

Program is telling me i am incorrect. >=[
So we start at the particles position and have wherever the velocity vector is pointing as the positive direction right?

The problem asks to rank the magnitude of the change.
You need the projection of the acceleration vector onto the direction of the velocity vector. It is the dot product of the acceleration vector with the velocity vector divided by the magnitude of the velocity vector.

 

[ehild]

It is easy to draw the orthogonal projection of the acceleratiom vector onto the direction of the velocity vector I show you for case A,

$\vec v = (2;-2)$ $\vec a = (0;4).$
$a*cos(\theta)= \frac{\vec a \cdot \vec v}{|v|}$

 

[isukatphysics69]

It is easy to draw the orthogonal projection of the acceleratiom vector onto the direction of the velocity vector I show you for case A,
View attachment 220697
$\vec v = (2;-2)$ $\vec a = (0;4).$
$a*cos(\theta)= \frac{\vec a \cdot \vec v}{|v|}$

Ok i appreciate this, let me give this another try and then come back. I do not understand why we are dividing by the velocity vector magnitude tho. what purpose is that for? I'm sorry i am really terrible with physics

 

[isukatphysics69]

I have the values A=2.12 C=0 E=0.89 F=2.236 D= Division by 0 doesn't exist B = motion is impossible

 

[isukatphysics69]

ok i think i understand why we divide by the magnitude of the velocity vector. it is because we are adding that value onto the velocity vector correct? So those values that i posted are the values being added onto the velocity vector to lengthen it. but i entered the answer F>A>E>C and it was incorrect

 

[ehild]

The acceleration has component parallel with the velocity and perpendicular to it. Only the parallel component changes the speed v, magnitude of the velocity. The other is the centripetal acceleration, it changes the direction of the velocity. a cos (ϑ) is the parallel component of the acceleration. .$a cos (ϑ)= \frac{a v cos(ϑ)}{v} = \frac{\vec a\cdot \vec v}{v}$
See the picture in Post #16. Can you read the parallel component of the acceleration ( parallel with the velocity)?
Can you calculate the dot product of the velocity and acceleration?

 

[isukatphysics69]

The acceleration has component parallel with the velocity and perpendicular to it. Only the parallel component changes the speed v, magnitude of the velocity. The other is the centripetal acceleration, it changes the direction of the velocity. a cos (ϑ) is the parallel component of the acceleration. .$a cos (ϑ)= \frac{a v cos(ϑ)}{v} = \frac{\vec a\cdot \vec v}{v}$
See the picture in Post #16. Can you read the parallel component of the acceleration ( parallel with the velocity)?
Can you calculate the dot product of the velocity and acceleration?

Yes, so it will be (2*0+4*(-2))/(sqrt(8)) = -2.828

 

[ehild]

Yes, so it will be (2*0+4*(-2))/(sqrt(8)) = -2.828

Yes, but you need only the magnitude, 2.828.
Look at C. What is the parallel component of the acceleration? What angle do the velocity and acceleration enclose?

 

[isukatphysics69]

A = (2*0+4*(-2))/(sqrt(8)) = -2.828 =2.828
B = MOTION IMPOSSIBLE there is no acceleration
C= (2*-1+1*-2)/sqrt(5) = 0
D = indeterminate form division by 0 since velocity = 0 there
E = (2*-1+0*2)/2 = -1 = 1
D = (3*2+-1*1)/sqrt(5) = 2.236

A>D>E>C
​

 

[isukatphysics69]

A = (2*0+4*(-2))/(sqrt(8)) = -2.828 =2.828
B = MOTION IMPOSSIBLE there is no acceleration
C= (2*-1+1*-2)/sqrt(5) = 0
D = indeterminate form division by 0 since velocity = 0 there
E = (2*-1+0*2)/2 = -1 = 1
D = (3*2+-1*1)/sqrt(5) = 2.236

A>D>E>C
​

Program saying this is wrong answer.

 

[ehild]

A = (2*0+4*(-2))/(sqrt(8)) = -2.828 =2.828
B = MOTION IMPOSSIBLE there is no acceleration
C= (2*-1+1*-2)/sqrt(5) = 0
D = indeterminate form division by 0 since velocity = 0 there
E = (2*-1+0*2)/2 = -1 = 1
D F= (3*2+-1*1)/sqrt(5) = 2.236

A>D>E>C
​

D = indeterminate form division by 0 since velocity = 0 there

If the velocity is zero, the rate of change of the speed is equal to the acceleration.

 

[isukatphysics69]

Yes, but you need only the magnitude, 2.828.
Look at C. What is the parallel component of the acceleration? What angle do the velocity and acceleration enclose?

90 degree angle, if it is

If the velocity is zero, the rate of change of the speed is equal to the acceleration.

YES THANK YOU!

 

[isukatphysics69]

If the velocity is zero, the rate of change of the speed is equal to the acceleration.

Thank you so much!