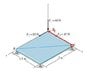
The discussion centers on understanding the position vectors r1, r2, and r3 in relation to torque calculations. The participant struggles with the notation, specifically why r1 is represented as -1.5j and r2 and r3 are zero. Clarification is provided that r2 and r3 equal zero because they intersect at points A and B. The conversation also touches on the definition of torque, emphasizing that it is calculated using the cross product of the position vector and the force vector. The distinction between torque about a point and about a fixed axis is highlighted, noting that the parallel component of the moment remains constant regardless of the point chosen on the axis.