Relative Motion of a Motorcyclist on a Rotating Bike

[usn7564]

Homework Statement

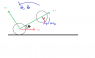
A motorcyclist accelerates rapidly so the bike entirely rests on the back wheel, while the midpoint of the back wheel O' accelerates with constant acceleration a_o' horizontally.
The entire bike rotatoes with angular velocity \frac{d}{dt} \theta and angular acceleration \frac{d^2}{dt^2} \theta, while the forward wheel rotates with constant angular velocity \omega_o. The distance between the wheel axis is l. Observe the point A, note that the radius is perp. to e_x', and find the velocity and acceleration relative to the ground.
O's velocity is given by \bar{v}_{o'}

Homework Equations

\bar{v} = \bar{v}_{sp} + \bar{v}_{rel}

\bar{v}_{sp} = \bar{v}_{o'} + \bar{\omega} \times \bar{r}_{rel}

The Attempt at a Solution

I've found v_sp without any issues (inserting into formulas, essentially) but run into problems at v_rel. It should be given by -(\frac{d}{dt} \theta + \omega_0)r\bar{e}_{x'}.
I don't understand how to get there at all, why would the relative velocity depend on the angular velocity of the entire bike at all? The coordinate system follows the bikes rotation so to my mind only the angular velocity of the wheel should matter for the point A. But if it depends on both of those how come they have the same sign? They are in opposite direction relative to each other. To add to that, as we have the angular velocity of the entire bike shouldn't the distance from the origin to A also matter?

Honestly not sure how to get the relative velocity when the point is rotation relative to the coordinate system.

 

[haruspex]

why would the relative velocity depend on the angular velocity of the entire bike at all? The coordinate system follows the bikes rotation so to my mind only the angular velocity of the wheel should matter for the point A. But if it depends on both of those how come they have the same sign? They are in opposite direction relative to each other. To add to that, as we have the angular velocity of the entire bike shouldn't the distance from the origin to A also matter?

Wrt sign, that's a matter of how you've interpreted the data. Unless otherwise stated, I would interpret all rotations in the same sense, but you've taken θ and ω₀ to be in opposite senses.
It's not clear to me whether ω₀ is supposed to be relative to the bike frame or relative to the ground. Would that explain it?

 

[usn7564]

Yeah was getting lost in what's relative to what. My directions for the anglular velocities were correct, basically what I was missing was that if the wheel didn't have its 'own' rotation
\omega_0 = 0

And the bike stands up on its back wheel the vector r->A will have the same direction (0, -r) unless there's friction (which there isn't in this ideal case). Then A will have rotated as much as the bike has, but in the opposite direction, relative to the bike frame that is.