itsagulati
- 15
- 0
Homework Statement
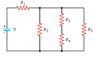
The circuit in the drawing contains five identical resistors. The V = 50 V battery delivers 46 W of power to the circuit. (Picture should show up somewhere)
Q: what is the resistance in each resistor
Homework Equations
so far the only things i have thought of is P = IV...which gives me I...and I = V/R
The Attempt at a Solution
I use the above equations to get to a Total resistance of 54.3 ohms...
i thought of several different ways to go about it from there and none of them have worked. dividing by 5 not going to work...
tried multiplying by 4 and dividing by 5 (5 total resistors, but when we add them in parallel we only have 4 being added into the total since two are in series).
anyways...basically i am lost...i've gotten through all 17 problems on the homework and cannot really think this one through...its 3:30 a.m...any help would be GREATLY appreciated!
Thanks!