SUCRALOSE
- 12
- 1
Homework Statement
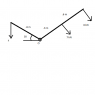
Determine the magnitude of F if the resultant of the three forces passes through point O.
Homework Equations
ƩFx = 0
ƩFy = 0
ƩM = 0
The Attempt at a Solution
The most I can come up with is that the two forces on the left would equal F on the right, and trying to ratio the force and distance it still does not work.
Any hints would be greatly appreciated.