MrMechanic
- 46
- 0
Homework Statement
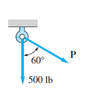
The resultant of the two forces has a magnitude of 650 lb. Determine the
direction of the resultant and the magnitude of P.
[See Attachment for Figure]
Homework Equations
Well, I only know is R^2=Fx^2+Fy^2
im still confused by this problem
The Attempt at a Solution
I tried using cosine law but it doesn't work well since the answer in the back is
(a) 71.8 degrees and (b) 235lb
Can someone help me?
Very Much appreciated.