Rotating Cylinder placed on rough surface

[thepopasmurf]

Homework Statement

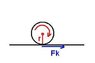
A cylinder is rotating about its axis and is placed on a rough surface. Find out what fraction of the initial Kinetic energy is lost due to sliding friction before the cylinder rolls smoothly.

Homework Equations

1/2 m v^{2} + 1/2 I \omega ^{2} = KE

rough surface -> v=\omegar
moment of inertia of cylinder is 1/2mr^{2}

The Attempt at a Solution

I don't really have an attempt because I am not convinced why there should be energy lost due to friction. If I weren't told that I would just equate the initial KE and the final KE and find the relationship between \omega_{i} and \omega_{f}

The answer should be 2/3

 

[Rick88]

I don't really have an attempt because I am not convinced why there should be energy lost due to friction.

Well, you're letting an object move on rough surface.
Surely you see that if you throw your slipper on the floor, it would stop moving after it traveled for some time.

 

[thepopasmurf]

Well, the question concerns the transition between rotating in free space and rotating on a rough surface. Apparently there is sliding friction when this happens. I am assuming that in the final state of the system, the cylinder is rolling smoothly with constant velocity.

 

[ehild]

Originally the cylinder had only rotational kinetic energy. Placing it on the rough surface, there is sliding friction acting on it. This force has torque: the torque decreases rotation. The force accelerates the linear motion of the centre of mass. When the cylinder rolls, the velocity of the CM is equal to the linear velocity of the rim.

Write the equation of motion both for the translation and for the rotation and find the time when v_CM=rω. Then calculate the sum of the translational and rotational KE.

ehild

 

[thepopasmurf]

Thanks, I didn't actually consider the problem on a force level, I assumed it could be done via energy methods.

 

[ehild]

Thanks, I didn't actually consider the problem on a force level, I assumed it could be done via energy methods.

The energy is not conserved. How do you apply energy methods?

ehild