bilgek33
- 12
- 0
I need to solve the following second order nonlinear differential equation:
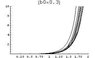
z''(b) * [6(1 - f)z(b) + (1+f)b z'(b)] = (15 - 9 f)[z'(b)]^2 + [2(1 - f) z(b) z'(b)] / b + [4 f z'(b)^(5/2)] / b^(1/2)
where f is a constant between [0,1].
initial conditions are z(0)=0 and z'(0)=0
I couldn't solve it analytically (except for f = 1 case). I tried numerical solution but my initial conditions have singularity.
In case, here is the more detailed Pdf file for the equation:
http://www.people.virginia.edu/~bk5w/home_files/trouble.pdf
I don't know whether this is a singularity of first kind of the second.
I wonder whether you guys can help me to solve this problem.
Thanks
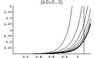
z''(b) * [6(1 - f)z(b) + (1+f)b z'(b)] = (15 - 9 f)[z'(b)]^2 + [2(1 - f) z(b) z'(b)] / b + [4 f z'(b)^(5/2)] / b^(1/2)
where f is a constant between [0,1].
initial conditions are z(0)=0 and z'(0)=0
I couldn't solve it analytically (except for f = 1 case). I tried numerical solution but my initial conditions have singularity.
In case, here is the more detailed Pdf file for the equation:
http://www.people.virginia.edu/~bk5w/home_files/trouble.pdf
I don't know whether this is a singularity of first kind of the second.
I wonder whether you guys can help me to solve this problem.
Thanks
Last edited by a moderator: