zaurus
- 18
- 0
Homework Statement
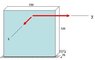
I have attached a figure showing beam bending around 2 axis. I need to calculate section modulus Sx and Sy but seem to be getting the major and minor axis confused. I guess the problem comes in when I go to select which term is squared in my equation below.
Homework Equations
S = 1/6 * b * h^2 for rectangular cross section
The Attempt at a Solution
Sx = (70*750^2)/6 = 6.56E+6
Sy = (750*70^2)/6 = 6.13E+5
If this is correct, could you please help clarify why b and h are what they are in the section modulus equation for 1) major axis and 2) minor axis.
Thanks.
Attachments
Last edited: