truettct
- 8
- 0
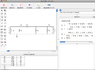
Simple Circuit: Find "v1" and "v2"
Using the circuit attached find the value of "v1" and "v2".
The values for
Is1=2.9A
R1=124 ohm
R2= 24 ohm
R3= 240 ohm
R4= 380 ohm
Is2= 3.2A.
I approached this problem by putting R3 and R4 in parallel and setting the two unknown potentials as potentialm and potentialn. I put these potentials on either side of the R2 resistor.
With these two unknown potentials I was able to set up these two equations
for potentialm:
-Is1 - (potentialm / R1) + ((potentialn - potentialm) / R2)=0
for potentialn:
Is2 - (potentialn / R34) - ((potentialn-potentialm) / R2)=0
Working out these equations and using algebra to solve for the potentials I get that potential m is 13.22V which is wrong, so there is no need to plug in for potential n.
Can someone help and show me where I went wrong or if I set up the equations wrong.
Thanks
Homework Statement
Using the circuit attached find the value of "v1" and "v2".
The values for
Is1=2.9A
R1=124 ohm
R2= 24 ohm
R3= 240 ohm
R4= 380 ohm
Is2= 3.2A.
Homework Equations
I approached this problem by putting R3 and R4 in parallel and setting the two unknown potentials as potentialm and potentialn. I put these potentials on either side of the R2 resistor.
With these two unknown potentials I was able to set up these two equations
for potentialm:
-Is1 - (potentialm / R1) + ((potentialn - potentialm) / R2)=0
for potentialn:
Is2 - (potentialn / R34) - ((potentialn-potentialm) / R2)=0
The Attempt at a Solution
Working out these equations and using algebra to solve for the potentials I get that potential m is 13.22V which is wrong, so there is no need to plug in for potential n.
Can someone help and show me where I went wrong or if I set up the equations wrong.
Thanks