1901phoenix
- 2
- 0
Simple electric force problem with point masses... includes picture!
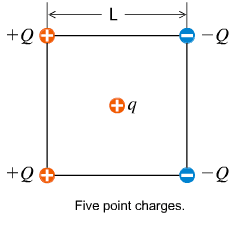
Four point charges of +/- q are arranged on the corners of a square of side L as illustrated in the figure. What is the net electric force that these charges exert on a point charge q placed at the center of the square (in terms of Q, q, L, and the Coulomb constant, K)
Diagram:
Coulomb's law: F= k * (q * q)/r^2
I started off my drawing a free body diagram. Picking one Q (the lower left) I drew one electrostatic force (from the upper Q) going vertically downwards because they are like charges so they have to repel.
I drew another electrostatic force (from the Q to the right, with the negative charge) going to the right in the x direction.
There is also going to be a force from Q on q in the center.
From here I am totally confused. I think if I am able to resolve all of the forces for one of the Q's I can use symmetry to find my answer but I am not sure how. I am also wary of how to relate any of the Q's to q. I hope this isn't too confusing for anyone, I really appreciate it.
Homework Statement
Four point charges of +/- q are arranged on the corners of a square of side L as illustrated in the figure. What is the net electric force that these charges exert on a point charge q placed at the center of the square (in terms of Q, q, L, and the Coulomb constant, K)
Diagram:
Homework Equations
Coulomb's law: F= k * (q * q)/r^2
The Attempt at a Solution
I started off my drawing a free body diagram. Picking one Q (the lower left) I drew one electrostatic force (from the upper Q) going vertically downwards because they are like charges so they have to repel.
I drew another electrostatic force (from the Q to the right, with the negative charge) going to the right in the x direction.
There is also going to be a force from Q on q in the center.
From here I am totally confused. I think if I am able to resolve all of the forces for one of the Q's I can use symmetry to find my answer but I am not sure how. I am also wary of how to relate any of the Q's to q. I hope this isn't too confusing for anyone, I really appreciate it.