Bluestribute
- 192
- 0
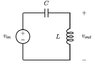
Homework Statement
Find a differential equation that describes the circuit that includes only vin and vout as variables.
Homework Equations
C(dvin - dvout)/dt = i
vin - vout = L(di/dt)
The Attempt at a Solution
So the answer I got was:
C(d2vout/dt2) + vout = LC(d2vin/dt2)
My question is, is it allowable to break up the capacitor derivate like that? After substituting in for i, I got:
vout = Ld/dt(C(dvin - dvout)/dt)
Then I broke up the capacitor into vin and vout terms and just rearranged. But I'm not 100% sure if that's legal.