Simple inclined plane reaction question, I need a debate solved

Join the discussion
Registration is free. Ask a follow-up in this thread, or start your own.
Sign up Log in
3 replies · 2K views
TyronLab
Messages
2
Reaction score
0

Homework Statement



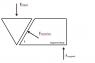
Two bodies are acting on one another on an inclined surface. Assuming a constant vertical input force and the lower body being vertically fixed in place on the right hand side, what will the angle of the inclined surface affect. In essence, will the vertical component of the reaction force on the supporting body's inclined face be constant with the angular reaction force increasing as the inclined angle theta increases, or will the reaction force be constant and its vertical component decrease as the angle theta increases?

The Attempt at a Solution



The two proposed solutions are mentioned above. We've got a debate running in our office about which one is correct, and I would like a solution if possible.

Thanks!

Oh and this is my first post.
 

Attachments

  • Untitled.png
    Untitled.png
    3.8 KB · Views: 459
Physics news on Phys.org
That diagram is just a simplification. The actual product is a cylinder with a chamfer cut out of it on the outer edge, and the supported body is a plate with a hole in the centre with a corresponding angle chamfered out of it.

I've uploaded a new attachment which represents a section view of the part we're actually concerned with.

So friction in this case isn't important, as the upper body is supported by the lower one without friction.

I hope this diagram is more explanatory.
 

Attachments

  • Untitled.png
    Untitled.png
    7 KB · Views: 444
TyronLab said:
That diagram is just a simplification. The actual product is a cylinder with a chamfer cut out of it on the outer edge, and the supported body is a plate with a hole in the centre with a corresponding angle chamfered out of it.

I've uploaded a new attachment which represents a section view of the part we're actually concerned with.

So friction in this case isn't important, as the upper body is supported by the lower one without friction.

I hope this diagram is more explanatory.
Oh OK, I get it. From equilibrium considerations in the vertical direction, the vertical component of the reaction force on the supporting body's inclined face will be constant, and the normal reaction force perpendicular to the incline will be increasing as the inclined angle theta increases. As the inclined angle decreases, the vertical component of the reaction force still says the same, but the normal reaction force then decreases.

So as I see it, whoever chose option 1 wins the debate.