So what is the limit of [cot(x)]^2 as x approaches infinity?

[Avi1995]

Using L'hospitals rule, find the limit

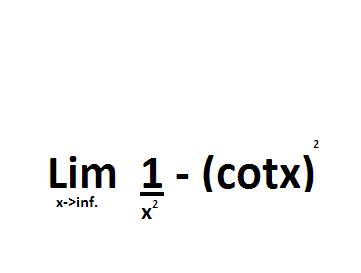
L' hospital rule
I seem to stuck using L'hospital's rule ,the derivatives of even 4th order are not simplying things.

 

[Spinnor]

You might have more luck over in Calculus & Beyond,

https://www.physicsforums.com/forumdisplay.php?f=156

If you plot [cot(x)]^2 (you may need a free plugin)

http://www.wolframalpha.com/input/?i=plot+[cot%28x%29]^2&cdf=1

it oscillates between 0 and infinity, does not seem like it tends towards anything as x --> infinity.