Sunny16
- 2
- 0
Homework Statement
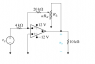
The op-amp in the circuit shown is ideal (please see attachment). The adjustable resistor RΔ has a maximum value of 160 kΩ and α is restricted to the range of 0.22 ≤ α ≤ 0.7.
(a) Calculate the range of vo if vg = 40 mV
(b) If α is not restricted, at what value of α will the op amp saturate?
Homework Equations
for a difference amplifier: vo = -(Rf/Ri)vin
The Attempt at a Solution
Firstly, I don't understand how the adjustable resistor functions in this circuit.
My interpretation is that the resistance ranges from a minimum of 0.22(160 kΩ / 0.7)
to a maximum of 160 kΩ (given).
PART A:
for maximum gain, Rf is maximized
so Rf = 20k + 160k = 180k
then vo = -(180/4)(40mV) = -1.8 V, which is not the right answer
for minimum gain, Rf = 20k + 50.29k = 70.29k
so vo = -(70.29/4)(40mV) = -0.703 V, which is again not the right answer
PART B:
for saturation, we would require a gain: A = 12V/40mV = 300
so Rf should be 300*4 kΩ = 1200 kΩ
then the variable resistor should provide a resistance of 1180 kΩ
how is this even possible, if the maximum resistance is way smaller than this value?
I must be misunderstanding how the resistor works, so I would appreciate any help
Thanks in advance.
Attachments
Last edited: