Solve for Tension in A-Shaped Ladder

[TastyTyr]

Torque HELP!

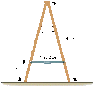
The drawing shows an A-shaped ladder. Both sides of the ladder are equal in length. This ladder is standing on a frictionless horizontal surface, and only the crossbar (which has a negligible mass) of the "A" keeps the ladder from collapsing. The ladder is uniform and has a mass of 12.0 kg. Determine the tension in the crossbar of the ladder.
This is what I did:
I took gravity and multiplied by 1.00 m and then multiplied by cos 75. I didvided this value by 4.00m*sin 75...I'm completely wrong help!
[(9.8)(1)(cos 75)]/[(4)(sin75)
The picture is attached***

 

[Astronuc]

I took gravity and multiplied by 1.00 m.

This is not correct.

The pivot point is at the apex of the ladder. The weight acts at the feet attempting to spread the legs apart at the base - moment arm = 4 feet.

The cross brace is 1 ft from the ends, but 3 feet from the pivot point.

 

[ceptimus]

Concentrate on the left or right side of the ladder and ignore the other side.

The vertical reaction from the floor has to support the weight of that half of the ladder. The weight of the ladder half acts vertically down, and as the ladder is uniform, the weight can be treated as a single force half way up the ladder.

Now you calculate the horizontal separation of the foot of the ladder from the center of the one half of it and you have a force and a distance; that gives you the torque.

Then to get the tension in the crossbar, you divide that torque by the vertical distance from the crossbar to the pivot point (the top of the ladder).