cristina045
- 3
- 0
Homework Statement
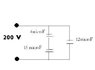
For the cicuit shown, the voltage is 200V, C1= 4microF, C2= 15microF and C3= 12microF
(i drew it on paint)
Find
a) the equivalent capacitance between the terminals
b) the charge stored on each capacitor
c) the total stored energy
Homework Equations
Ceq= 1/c1 + 1/c2 +1/c3
or
Ceq = C1+C2+C3
C=Q/V
I think this is the right equation for the energy stored in a capacitor:
U= QV/2=CV^2/2
The Attempt at a Solution
Ok I'm really not sure because I'm having a lot of trouble with figuring circuits out. I think C1 and C2 are in series but in parallel with C3. For a) what i did is :
Ctot = 1/Ceq + C3
and
1/Ceq = 1/C1 + 1/C2
Therefore Ct = 3.15microF + 12microF
Ct= 15.15microF
b) I would use C= Q/V
so Q1 = 8*10^-4 C
Q2= 3*10^-3 C
Q3= 2.4*10^-3 C
c) U=CV^2/2
my equivalent capacitance was 15.15microF and my voltage was 200v, therefore my U should be 0.303J
It seems to me that b and c were too easy to get. Besides, I'm not even sure my a) part is right. I'm so confused...
the picture i drew is at the bottom, it's just pending approval.
Attachments
Last edited: