Solving a Circuit Problem with Ideal Batteries: Finding Energy Dissipation Rate

[Silimay]

I have a circuit problem I'm having trouble with. I've attached an image of it.

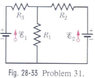
Emf_1 = 3 V; Emf_2 = 1 V; R_1 = 5 \Omega; R_2 = 2 \Omega; R_3 = 4 \Omega

Both batteries are ideal. a.) What is the rate at which energy is dissipated in R_1?

Since P = i^2R, I figured that I should find the current. I used the loop rule (I'm not sure if I should have done this or not). I started at a point between emf_1 and R_3. I pretended the current was pointed downward at emf_1 and upward through R_1 and R_2. I called those last two currents i_1 and i_2, respectively. i_{total} = i_1 + i_2.

For the inside (left) loop:

R_3i_{total}+R_1i_1+emf_1 = 0

For the outside loop:

R_3i_{total} + R_2i_2-emf_2+emf_1 = 0

+R_3(i_1+i_2)+R_1i_1 = -emf_1

-R_3(i_1+i_2)-R_2i_2+emf_2=-emf_1

(5\Omega)i_1-(2\Omega)i_2 = -7 V

-(4\Omega)(i_1+i_2)-(2\Omega)i_2 = -3 V

-(4\Omega)i_1-(6\Omega)i_2 = -3 V

I solved the system of equations and ended up with i_1 = 0.95 A. This isn't the correct answer, because i^2R ends not equalling 0.346 W, which is the right answer.

I have the feeling I did something really wrong. Did I make it way too complicated? I have a tendency to overdo things

~Silimay~

 

[jamesrc]

Hi,

Two things I can see:

- With the way you defined things and the way you are going around your loops, the signs on your voltages should be switched (e.g. first loop eq should be R₃i_total-ε₁+R₁i_i = 0).

- I think you made some algebra mistakes after that.

Try again and I think you'll get it.

 

[wais]

Hi Silimay,

Thank you for sharing your circuit problem and your approach to solving it. It seems like you have the right idea in using the loop rule to find the current, but there are a few things that may have caused your incorrect answer.

Firstly, when applying the loop rule, it is important to make sure that the direction of current and the signs of the emf and resistances are consistent. In your equations, it seems like you have used the opposite sign for the emf_1 term in the first equation, which would result in a different answer for i_1.

Secondly, when solving a system of equations, it is important to double check your calculations and make sure all the variables are accounted for. In your final equation, you have only solved for i_1, but the question asks for the rate at which energy is dissipated in R_1, which involves both the current and the resistance. You will need to use the value of i_1 you have found and the resistance of R_1 to calculate the power dissipated in R_1.

Lastly, it is always a good idea to check your answer using basic physics principles. In this case, you can use the formula P = i^2R to calculate the power dissipated in R_1 and compare it to the answer given. If they do not match, it is likely that there is an error in your calculations.

I hope this helps you to understand where you may have gone wrong in your approach. Remember to always double check your work and use the correct signs and directions when applying equations in physics problems. Keep practicing and you will become more confident in solving circuit problems!