- #1
ApeXaviour
- 35
- 0
I was fine with these in class, tutorials etc. It's only since I found this in a past paper that I've had a problem with them.
[tex]\[ \int_0^1\! \int_{\sqrt{y}}^1 9\sqrt{1-x^3}\,dxdy.\]
[/tex]
Nomatter what I substitute in under the sqrt sign I just can't get out the integral for x :(
I tried changing the limits so they run from x^2 to 1 for y and 0 to 1 for x..
I'm having similar trouble with this one...
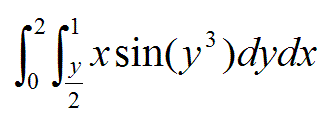
The Sin(y^3) here is what's getting me. Also tried changing the limits and substitution. No luck.. just ends up a big unsolvable mess for me
Thanks
Declan
[tex]\[ \int_0^1\! \int_{\sqrt{y}}^1 9\sqrt{1-x^3}\,dxdy.\]
[/tex]
Nomatter what I substitute in under the sqrt sign I just can't get out the integral for x :(
I tried changing the limits so they run from x^2 to 1 for y and 0 to 1 for x..
I'm having similar trouble with this one...
The Sin(y^3) here is what's getting me. Also tried changing the limits and substitution. No luck.. just ends up a big unsolvable mess for me
Thanks
Declan
Attachments
Last edited: