Solving Rod Slipping: Find x min with Tension & Friction

[eliassiguenza]

Homework Statement

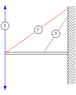
a uniform rod of length 4.0m of mass M is supported by a cable which is under tension T. The other end rests against as wall, where it is held by friction. The coefficient of static friction is 0.5. An additional mass M is hung from the rod at a distance x from the wall

Homework Equations

Mgx + 2 Mg = 4T sinӨ
2Mg = (R/2) + T sin Ө
R = T cos Ө

The Attempt at a Solution

Solve the above three equations simultaneously for Ө = 37 to obtain the minimum value of x in metres where the additional mass M may be hung without causing the rod to slip.

Answer is : x min = 2.8 m

how do you solve this ? I am totally lost :'( please help I have an exam on monday next week :'(

 

[wbandersonjr]

Mgx + 2 Mg = 4T sinӨ
2Mg = (R/2) + T sin Ө
R = T cos Ө

The first equation looks good. How did you get the other two? The second looks like the equilibrium equation for the forces in the vertical direction, but it has mistakes in it.

 

[Quinzio]

The cable is horizontal ? Or is the rod horizontal ?
The additional mass "M" is equal to the rod mass "M" ?

 

[gneill]

The problem would be greatly clarified if a diagram could be provided. The orientation and location of attachment of the cable are unspecified, so the problem is not solvable.

To the OP: Do any of the cable positions, 1, 2, or 3 in the attached figure, correspond to the current problem?

 

[eliassiguenza]

yes that's the diagram how silly of me! oh god i forgot... yeah that's the one! cable one is just like the red one