Solving Upright Rod Falling Problem

[Karol]

Homework Statement

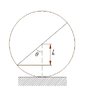
An upright standing rod of mass m and length 2l receives a small push at the top and falls.
The floor is smooth. the height of the center of mass at any given time is h, according to the drawing.
Show that the velocity of it's center of mass is:
$$V=(l-h)\sqrt{6g(l+h)/(4l^2-3h^2)}$$

Homework Equations

$$M=I\alpha$$

The Attempt at a Solution

Because all forces are vertical, I assume the center of mass will move directly vertical, under it's initial location, as in the drawing.
The horizontal distance between the reaction of the floor F and the center of mass is:

$$x=lcos\theta=l \sqrt{1-sin^2\theta}=l \sqrt{1-\frac{h^2}{l^2}}=\sqrt{l^2-h^2}$$

$$\left\{\begin{array}{l}mg-F=ma\\F\sqrt{l^2-h^2}=\frac{4}{3}ml^2\alpha \\a=\alpha l\end{array}$$

From those:

$$a=\frac{3g\sqrt{l^2-h^2}}{4l+3\sqrt{l^2-h^2}}$$

And now:

$$V=\int_{l}^{h}\frac{3g\sqrt{l^2-h^2}}{4l+3\sqrt{l^2-h^2}}dh$$

Which, I tried, doesn't yield the required result.

 

[tiny-tim]

Hi Karol!

(have a theta: θ and an alpha: α and a square-root: √ )

a is not αl

(also, conservation of energy might be easier )

(and you could have got x = √(l² - h²) directly from Pythagoras!)

 

[Karol]

I don't understand:

(have a theta: θ and an alpha: α and a square-root: √ )

a is not αl

in my equations, a is the vertical (down) acceleration. What do you mean by al?
Does your a have the meaning of acceleration, or something else?

 

[tiny-tim]

a is not alpha times l

 

[Karol]

I tried:
$$h=l\sin\theta\Rightarrow\dot{h}=l\dot{\theta}\cos\theta\Rightarrow\ddot{h}=l\left(\ddot{\theta}\cos\theta-\dot{\theta}\sin\theta\right)$$
Together with:
$$mg-F=m\ddot{h}$$

And:
$$M=I_c\ddot{\theta}\Rightarrow F\sqrt{l^2-h^2}=\frac{1}{12}m(2l)^2\ddot{\theta}$$

I can't get anything.

 

[tiny-tim]

h' = lθ'cosθ => h'' = l(θ''cosθ - θ'²sinθ)

BUT I seriously suggest that you use conservation of energy …

that only involves θ', with no θ'', which is obviously easier,

and it gives you the required answer for V directly

 

[Karol]

Energy:
$$mgl=mgl\cdot\sin\theta+I_c\ddot{\theta}^2$$
I can't solve it for the function $\theta(t)$.

 

[tiny-tim]

uhh?

how did you get θ'' into the energy?

(and how did you get g twice?)

start again ​

 

[Karol]

Correction:
$$mgl=mgl\cdot\sin\theta+I_c\dot{\theta}^2$$

The $mgl\cdot\sin\theta$ is the new height of C.M. while in motion

 

[tiny-tim]

what about 1/2 mv_c.o.m² ?

 

[Karol]

$$mgl=mgl\cdot\sin\theta+\frac{1}{2}m\dot{\theta}^2\cos^2\theta+ \frac{1}{2}I_c\dot{\theta}^2$$

 

[tiny-tim]

Yup!

Now write cosθ in terms of l and h, and that should give you the required equation for V.

 

[Marioqwe]

I am sorry but how did you derive the position for the center of mass?

Also, what does the M=I(alpha) represent?

 

[tiny-tim]

Hi Marioqwe!

(have an alpha: α )

I am sorry but how did you derive the position for the center of mass?

Also, what does the M=I(alpha) represent?

The rod is at angle θ to the ground, so the centre of mass is at height h = lsinθ.

M = Iα is usually written τ = Iα …

τ is the net torque , ie the moment of the external forces (presumably "M" stands for "moment"); I is the moment of inertia and α is the angular acceleration …

all should be measured relative to the centre of mass, or to a point stationary or moving parallel to the centre of mass (so, in this case, the base of the rod will not do).

 

[Karol]

I assume the rod is rotating round it's bottom since the forces are according to picture A, attached here.
If the forces were according to picture B-then it would have rotated round it's center, am I correct?
And knowing:
$$\sin\theta=\frac{h}{l}$$
then energy:
$$mgl=mgl\frac{h}{l}+\frac{1}{2}mV^2+\frac{1}{2}\frac{1}{3}4ml^2$$
Which doesn't give exactly the required V, the C.M. velocity.

 

[tiny-tim]

Hi Karol!

Your conservation of energy equation doesn't seem to have a 1/2 Iω² in it.

I assume the rod is rotating round it's bottom since the forces are according to picture A, attached here.
If the forces were according to picture B-then it would have rotated round it's center, am I correct?

Are you talking about the instantaneous centre of rotation?

If so, that's somewhere between the centre and the end of the rod (because the centre is moving down, and the end is moving to the left).

Anyway, always take moments about the centre of mass unless you're certain you know where the instantaneous centre of rotation is.

EDIT: oops, I got a bit confused … the option in that last sentence applies to τ = Iα equations.

For a conservation of energy equation, if you're using 1/2 mv² + 1/2 Iω², you must use the centre of mass.​

 

[Karol]

According to the new drawing, the height h is:
$$h=l\cos\theta\rightarrow\dot{h}=-l\dot{\theta}\sin\theta=-l\dot{\theta}\frac{h}{l} \rightarrow\dot{\theta}^2=-\frac{V^2}{h^2}$$
So:
$$mgl=mgl\frac{h}{l}+\frac{1}{2}mV^2+\frac{1}{2}\frac{1}{3}4ml^2\dot{\theta}^2= mgl\frac{h}{l}+\frac{1}{2}mV^2-\frac{1}{2}\frac{1}{3}4ml^2\frac{V^2}{h^2}$$
Which is not correct.
But it can not be correct since, you say, the instantaneous center of rotation changes it's place relative to the length of the rod all the time, so which I do I take?

 

[tiny-tim]

Why are you using a new diagram? You've changed θ for 90° - θ, and then forgotten you've done it!

(Also, you need I for the centre of a rod, not the end).

Try again. ​

 

[Karol]

Solved, thanks to you, Tiny-Tim.
I appreciate your dedication.

For a conservation of energy equation, if you're using 1/2 mv² + 1/2 Iω², you must use the centre of mass.[/INDENT]

Why, can't I take 1/2 Iω² around any point, for conservation of energy?

 

[tiny-tim]

Because energy of course is the same about any point …

about the centre of rotation it is 1/2 I_c.o.rω² …

about any other point you need a correction term

and the only convenient other point is the c.o.m. …

since I_c.o.r. = I_c.o.m. + mr_c.o.m.²,

that's also equal to 1/2 (I_c.o.m. + mr_c.o.m.²)ω²,

= 1/2 I_c.o.m.ω² + 1/2 mr_c.o.m.²ω²

= 1/2 I_c.o.m.ω² + 1/2 mv_c.o.m.² ​

(in other words: if you're using v_c.o.m., you must also use I_c.o.m.)

 

[Karol]

But can I use M=I$\alpha$ for a point other than the center of rotation?
I have tried it for a simple case and it works, I get the same $\alpha$.
And, if so, I can use E=1/2 mv_c.o.m.²+1/2I$\varpi$² for that point either, no?
So I don't have to use, necessarily, only:
E=1/2 mv_c.o.m.2+1/2I_c.o.m.$\varpi$²

 

[tiny-tim]

Hi Karol!

(What happened to that α and ω I gave you? )

But can I use M=I$\alpha$ for a point other than the center of rotation?
I have tried it for a simple case and it works, I get the same $\alpha$.

Which point?

And, if so, I can use E=1/2 mv_c.o.m.²+1/2I$\varpi$² for that point either, no?
So I don't have to use, necessarily, only:
E=1/2 mv_c.o.m.2+1/2I_c.o.m.$\varpi$²

For E, you can use any point, so long as you add a suitable correction term.

 

[Karol]

For E, you can use any point, so long as you add a suitable correction term.

You mean if I know the Moment of inertia I for that point, that's what you mean by correction factor, right?
I also ask weather I can calculate moments and I around a point other than the center of rotation and the center of mass in order to use M=I$\alpha$, providing, of course, I know I and M around that point.

 

[tiny-tim]

You mean if I know the Moment of inertia I for that point, that's what you mean by correction factor, right?

noooo

I also ask weather I can calculate moments and I around a point other than the center of rotation and the center of mass in order to use M=I$\alpha$, providing, of course, I know I and M around that point.

The point has to be stationary, or the centre of mass, or a point moving parallel to the centre of mass.

The base of the rod does not move parallel to the centre of mass, so you cannot use it for the τ = Iα equation (why do you keep writing "M"? ).