Special relativity of a triangle

[Niles]

Homework Statement

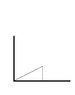
In rest, a triangle has sides 1, 1 and sqrt(2). Find the angles of the triangle. when it moves with speed c/2.

The Attempt at a Solution

I have found u_y and u_x - it's sin(45)*c/2 and cos(45)*c/2 - so I get the angles to be 45, 45 and 90 like before - but that can't be true?

 

[Doc Al]

How is the triangle oriented with respect to the direction of motion? (I presume that it moves in the +x direction, parallel to one of the sides of length 1.) Which sides undergo Lorentz contraction? What are the observed lengths of the sides parallel and perpendicular to the x-axis? Use that to calculate the new angles.

 

[Niles]

It moves in the direction of the longest side - so in 45 degrees.

Then both sides undergo Lorentz-contradiction - but since the speed before is 0, the Lorentz-factor is 1?

 

[Doc Al]

If I understand you correctly (a diagram would be nice!) the long side is on the x-axis (the direction of motion) and the other sides angle upwards and meet at a vertex along the y-axis.

The proper dimensions of the triangle are as given: 1, 1, sqrt(2). From the moving frame, what is the gamma factor? (It's not 1!)

So, does the height of the triangle change? Does the length of the long side change? Draw yourself a diagram of the triangle as seen in the moving frame and recompute the angles.

 

[Niles]

I believe the diagram is as attached.

The Lorentz-factor in the moving frame is 1/sqrt(1-v^2/c^2), where v = c/2.

So gamma = 2/sqrt(3), and the sides are L = L_0 * gamma?

 

[Doc Al]

I believe the diagram is as attached.

Can I assume that it's moving along the x-direction? (And not parallel to the long side, as stated earlier.)

The Lorentz-factor in the moving frame is 1/sqrt(1-v^2/c^2), where v = c/2.

Good.

So gamma = 2/sqrt(3),

Yes.

and the sides are L = L_0 * gamma?

No. The side parallel to the direction of motion will appear contracted: L = L_0/gamma.