Sphere rolling down an incline plane pulling a rope off a cylinder

[leeone]

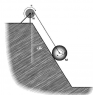
The tension in the rope is actually being provided by a solid sphere with radius 23.5 cm that rolls down an incline as shown in the figure. The incline makes an angle of 32° with the vertical. The end of the rope is attached to a yoke that runs through the center of the sphere, parallel to the slope. The friction between the incline and the ball is sufficient that the ball rolls without slipping. The mass of the sphere is closest to

I solved for the Tension in a previous problem to be T= 12.7 N

also angular acceleration of the cylinder is 12.5 rad/s^2 and its mass is 7.25 kg and its radius is 28cm.

I drew some free body diagrams and got

M=2T/((gsin(theta)-(7/5)R(angular acceleration of sphere)) and theta = 58 degrees...I just don't know how to get the angular acceleration of the sphere.

I tried to get it by equating the torques of the cylinder and sphere but then I needed the mass which is what I am solving for.

 

[Doc Al]

How can you relate the angular and linear acceleration?

 

[leeone]

linear acceleration = angular acceleration(R)

 

[leeone]

okay my equations I started with we're

Mgsin(theta)- friction-T=M(linear acceleration)

friction(R)-T(R)= (I of sphere)(angular acceleration)

 

[leeone]

but here I have three unknowns and two equations even if I know the above relation linear acceleration = (angular acceleration(R)

 

[Doc Al]

okay my equations I started with we're

Mgsin(theta)- friction-T=M(linear acceleration)

This one makes sense.

friction(R)-T(R)= (I of sphere)(angular acceleration)

The tension acts at the center of the sphere, so it does not produce a torque.

 

[Doc Al]

I solved for the Tension in a previous problem to be T= 12.7 N

How did you solve for the tension?

 

[leeone]

Using that T(R of cylinder) = I (angular acceleration of cylinder) = (1/2)(M of cylinder)(R of cylinder)^2(angular acceleration of cylinder)

 

[leeone]

It was a three question problem and the angular acceleration of the cylinder
was caused by the tension force...at this point they did not inform you the sphere was what was causing it.

 

[Doc Al]

Using that T(R of cylinder) = I (angular acceleration of cylinder) = (1/2)(M of cylinder)(R of cylinder)^2(angular acceleration of cylinder)

That's fine.

 

[Doc Al]

It was a three question problem and the angular acceleration of the cylinder
was caused by the tension force...at this point they did not inform you the sphere was what was causing it.

But they must have given you additional information.

In any case, once you have the tension, you should be able to determine the accelerations.

 

[leeone]

Assume that the pulley is at rest at time t0, which is the time that the tension in the rope is applied. The tension remains constant for 2.0 s at which point the rope goes slack, and the pulley continues to spin with no further force applied from the rope for an additional 3.0 s (for a total of 5.0 s of rotation). What, in radians, is the total angular displacement the pulley has undergone since t0?
a) 52 rad b) 83 rad c) 100 rad d) 160 rad e) 25 rad f) 180 rad

This is the only other information...but I was pretty positive this was unrelated to the questionIf they must have given me additional information then why do you say I should be able to determine the accelerations?

Also I am trying to solve for the mass

 

[Doc Al]

Assume that the pulley is at rest at time t0, which is the time that the tension in the rope is applied. The tension remains constant for 2.0 s at which point the rope goes slack, and the pulley continues to spin with no further force applied from the rope for an additional 3.0 s (for a total of 5.0 s of rotation). What, in radians, is the total angular displacement the pulley has undergone since t0?
a) 52 rad b) 83 rad c) 100 rad d) 160 rad e) 25 rad f) 180 rad

This is the only other information...but I was pretty positive this was unrelated to the question


If they must have given me additional information then why do you say I should be able to determine the accelerations?

Did they give you the tension? As stated, there is not enough information to answer that question. (They must have given you something.)

 

[leeone]

The tension is 12.7 N? which I solved for from the rotational acceleration of the cylinder...could I equat the torques of the two and solve for the angular acceleration of the sphere in terms of the angular acceleration of the cylinder?

 

[Doc Al]

The tension is 12.7 N? which I solved for from the rotational acceleration of the cylinder...could I equat the torques of the two and solve for the angular acceleration of the sphere in terms of the angular acceleration of the cylinder?

So they gave you the rotational acceleration of the cylinder?

If so, you can use it to find the rotational acceleration of the sphere. Hint: The linear acceleration of the rope is the same as the linear acceleration of the sphere.

 

[leeone]

yes they did. could I not use (I of sphere)*(angular acceleration of sphere)=(I of cylinder)*(angular acceleration of cylinder)?

 

[Doc Al]

could I not use (I of sphere)*(angular acceleration of sphere)=(I of cylinder)*(angular acceleration of cylinder)?

Not I, but R.

 

[leeone]

Thank You. I tried that previously but got the wrong answer b/c my calculator was in radians and not degrees -_____-

 

[Doc Al]

Thank You. I tried that previously but got the wrong answer b/c my calculator was in radians and not degrees -_____-

D'oh!