Spring block system with friction

[Saitama]

Homework Statement

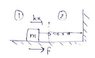
The block shown in the drawing is acted by a spring with spring constant $k$ and a weak friction force of constant magnitude $f$. The block is pulled a distance $x_0$ from equilibrium and released. It oscillates many times and eventually comes to rest.

a. Show that the decrease of amplitude is the same for each cycle of oscillation.

b. Find the number of cycles n the mass oscillates before coming to rest.

(Ans. $n=\frac{1}{4}[(kx_0/f)-1] \approx kx_0/(4f)$)

Homework Equations

The Attempt at a Solution

Let x be the displacement of block from the equilibrium position. Applying Newton's second law on the block,
$$m\frac{d^2x}{dt^2}=-kx-f$$
Solving the D.E
$$x(t)=A\sin(\omega t)+B\cos(\omega t)-\frac{f}{k}$$
where A and B are constants and $\omega^2=\frac{k}{m}$.
From the initial conditions, $A=0$ and $B=x_0+f/k$. Hence, the equation of motion is
$$x(t)=\left(x_0+\frac{f}{k}\right)\cos(\omega t)-\frac{f}{k}$$
I am stuck here. I guess the above equation is wrong. Part a of the question hints me that the amplitude of motion should have a time dependence. The amplitude I get is $x_0+f/k$ which is time independent.

Any help is appreciated. Thanks!

 

[TSny]

Does $f$ always act in the same direction?

Also, What direction does the friction act just after being released?

 

[Saitama]

Does $f$ always act in the same direction?

Thanks for the quick response.

Oh yes, it won't be in the same direction always. Then how should I approach the problem?

 

[Chestermiller]

You need to take into account that the friction force f changes direction each time x passes through a maximum or minimum (i.e., velocity is zero).

 

[TSny]

Maybe it will help to work out the first half of a cycle.

 

[Saitama]

(Sorry for the late reply, I had to leave at that time )

I am not sure so I will start with the FBDs. (The friction shown acts on the block, not on the ground, the dotted line shows the equilibrium position)

When the block is released from the initial position,

When the block enters the region 2,

The spring compresses to a maximum and the block starts to move towards left. While the block is in region 2, the fbd is as follows

When the body finally reaches back into region 1,

Are the FBDs correct? How should I form the equation of motion now? Should I separately apply the Newton's second law for each situation I have shown?

(Sorry for the awful images, its difficult to draw springs (for me) in the software I use, I hope they are not hard to interpret.)

 

[Chestermiller]

Your original differential equation is incorrect. There should be a +f, rather than -f. Redraw the figure with the x-axis pointing in its usual orientation, and you will see what I mean. Write out the correct solution to the differential equation. Then calculate the location of the block 1/2 cycle later when its velocity reverses direction. What is its location then? How much has the amplitude decreased during this half cycle. Does this decrease in amplitude depend on x₀? If not, then the amplitude will decrease by this same amount every half cycle.

 

[gneill]

You may find that an energy approach is fairly straightforward, rather than trying to write several differential equations to account for changing frictional force direction.

Suppose the spring is stretched leftward from equilibrium by $x_o$. The system is then "armed" with potential energy in the spring. When released, the block will move to some maximal location on the other side of the equilibrium point before springing back. Can you work out that distance by considering energy?

Do the same for the return journey.

 

[Saitama]

You may find that an energy approach is fairly straightforward, rather than trying to write several differential equations to account for changing frictional force direction.

Suppose the spring is stretched leftward from equilibrium by $x_o$. The system is then "armed" with potential energy in the spring. When released, the block will move to some maximal location on the other side of the equilibrium point before springing back. Can you work out that distance by considering energy?

Do the same for the return journey.

Yes, I think the energy approach is easier. Here's my attempt:
For the first half cycle,
$$\frac{1}{2}kx_0^2=f(x+x_0)+\frac{1}{2}kx^2$$
where x is the distance from the equilibrium point towards right.
Rearranging,
$$kx^2+2fx+2fx_0-kx_0^2=0$$
Solving the quadratic,
$$x=x_0-\frac{2f}{k}$$
It seems too much work to apply energy conservation for the next half cycle and solve the resulting quadratic. Can I simply state that the final distance of block from equilibrium point when it returns back towards left and reaches the position of maximum stretch is $x_0-\frac{4f}{k}$?

 

[TSny]

It seems too much work to apply energy conservation for the next half cycle and solve the resulting quadratic.

The final value of x for the first half cycle becomes x_o for the next half cycle. So you can repeat the same analysis for the second half cycle.

 

[gneill]

The final value of x for the first half cycle becomes x_o for the next half cycle. So you can repeat the same analysis for the second half cycle.

Absolutely! Or you just note that the loss of amplitude that occurred on the first half-cycle, 2f/k, did not depend upon the initial displacement. So the loss must be independent of the extension, and so you can validly make the loss per full cycle twice that, or 4f/k.

@Pranav-Arora: If you want to skip directly to the conclusion then you should present the reason why you can do it, namely by identifying the independence of the loss and extension. You want to avoid having a marker claim that an unjustified conclusion was stated.

 

[Chestermiller]

Yes, I think the energy approach is easier. Here's my attempt:
For the first half cycle,
$$\frac{1}{2}kx_0^2=f(x+x_0)+\frac{1}{2}kx^2$$
where x is the distance from the equilibrium point towards right.
Rearranging,
$$kx^2+2fx+2fx_0-kx_0^2=0$$
Solving the quadratic,
$$x=x_0-\frac{2f}{k}$$
It seems too much work to apply energy conservation for the next half cycle and solve the resulting quadratic. Can I simply state that the final distance of block from equilibrium point when it returns back towards left and reaches the position of maximum stretch is $x_0-\frac{4f}{k}$?

Just a minor correction: After half a cycle, the correct location is x = -x₀ + 2f/k.

 

[gneill]

Just a minor correction: After half a cycle, the correct location is x = -x₀ + 2f/k.

That would be the location assuming a coordinate system with origin at the equilibrium positon. But P.A.'s x is the extension to the right of the equilibrium position; equivalent to the magnitude of the displacement from equilibrium.

 

[Chestermiller]

That would be the location assuming a coordinate system with origin at the equilibrium positon. But P.A.'s x is the extension to the right of the equilibrium position; equivalent to the magnitude of the displacement from equilibrium.

According to the problem statement "The block is pulled a distance x₀ from equilibrium and released." From the diagram, in order to pull the block a distance x0 from equilibrium, it had to be displaced to the left by an amount x0.

 

[gneill]

According to the problem statement "The block is pulled a distance x₀ from equilibrium and released." From the diagram, in order to pull the block a distance x0 from equilibrium, it had to be displaced to the left by an amount x0.

Yes, when released it will travel to the right of equilibrium by some amount. We only need to know the magnitude of that amount. The block then returns to the left side of equilibrium, again with some magnitude of displacement. The setup for the return is the same as for the initial position except the displacement is smaller by some amount, so the "starting" PE is a bit smaller. It's the "loss" of displacement magnitude on the left side that we're interested in.

One could also do the problem keeping track of positions and force directions with respect to a fixed coordinate system, calculate the zero KE positions on each side with respect to that coordinate system, but energy being positive quantities (thanks to the "d²" in the PE terms) allows us to get away with magnitudes and use of symmetry for the second half-cycle.

 

[Chestermiller]

Yes, when released it will travel to the right of equilibrium by some amount. We only need to know the magnitude of that amount. The block then returns to the left side of equilibrium, again with some magnitude of displacement. The setup for the return is the same as for the initial position except the displacement is smaller by some amount, so the "starting" PE is a bit smaller. It's the "loss" of displacement magnitude on the left side that we're interested in.

One could also do the problem keeping track of positions and force directions with respect to a fixed coordinate system, calculate the zero KE positions on each side with respect to that coordinate system, but energy being positive quantities (thanks to the "d²" in the PE terms) allows us to get away with magnitudes and use of symmetry for the second half-cycle.

It seems to me we are saying the same thing, but, please understand that I was only trying to be more precise than the OP about expressing the solution to the equations. As you've noted, there are two approaches to solving the problem, both of which give the same answer. Below, I've presented my solution by each of the two methods. Please point out if I have made a mistake.

Let x be the displacement of the block from the equilibrium position, and let x₀ be the initial displacement of the block.

Force Balance Method (first half-cycle):
$$x=\left(x_0-\frac{f}{k}\right)\cos(\omega t)+\frac{f}{k}$$
After half a cycle,
$$x=-\left(x_0-\frac{f}{k}\right)+\frac{f}{k}=-x_0+2\frac{f}{k}=-\left(x_0-2\frac{f}{k}\right)$$

Energy Balance Method (first half cycle):
$$\frac{1}{2}kx_0^2-\frac{1}{2}kx^2=f(x_0-x)$$
Dividing both sides by $(x_0-x)$, we get:
$$\frac{1}{2}k(x_0+x)=f$$
Solving for x gives:
$$x=-\left(x_0-2\frac{f}{k}\right)$$
These results are in agreement with one another. Since x₀ is arbitrary, they show that the amplitude of the oscillation decreases by 2f/k every half cycle.

Chet

 

[Saitama]

How do I solve the b part? I can find the total distance covered by the block during the complete motion from energy conservation but I am really clueless about relating it with the number of cycles.

 

[gneill]

How do I solve the b part? I can find the total distance covered by the block during the complete motion from energy conservation but I am really clueless about relating it with the number of cycles.

How many times can you subtract a whole 4f/k from x_o ?

 

[Saitama]

How many times can you subtract a whole 4f/k from x_o ?

Till it becomes zero?

 

[gneill]

Till it becomes zero?

Till it becomes exactly zero (unlikely) or the next whole subtraction cannot be done without it going negative.

Think of each subtraction as the completion of one cycle, with what's left being the starting displacement for the next cycle. The block will not return to the left side of equilibrium if doing so would make the displacement negative...

 

[Saitama]

Till it becomes exactly zero (unlikely) or the next whole subtraction cannot be done without it going negative.

Think of each subtraction as the completion of one cycle, with what's left being the starting displacement for the next cycle. The block will not return to the left side of equilibrium if doing so would make the displacement negative...

I still don't understand what to do.

After n oscillations, the distance of block from the equilibrium position is:
$$x_0-\frac{4nf}{k}$$
Correct? Do you mean this should be greater than zero?

 

[gneill]

I still don't understand what to do.

After n oscillations, the distance of block from the equilibrium position is:
$$x_0-\frac{4nf}{k}$$
Correct? Do you mean this should be greater than zero?

Yes. Consideration of the "end game", where the remaining amplitude is smaller than the amount you want to subtract for a cycle leads to the "-1" in the given answer. But if the friction is small and the total number of oscillations is high, the "-1" is probably buried by other uncertainties and will be lost to significant figures.

 

[Saitama]

Consideration of the "end game", where the remaining amplitude is smaller than the amount you want to subtract for a cycle leads to the "-1" in the given answer.

The distance of block from equilibrium after (n-1) oscillations is
$$x_0-\frac{4(n-1)f}{k}$$
How do you know that its less than 4f/k?

 

[gneill]

If you start with a real number X and take chunks of size d out of it, you can get n = INT(X/d) full chunks out of it. The remainder of X/d is not a full "d-sized" chunk.

 

[Saitama]

If you start with a real number X and take chunks of size d out of it, you can get n = INT(X/d) full chunks out of it. The remainder of X/d is not a full "d-sized" chunk.

x_0-4nf/k should be greater than or equal to zero i.e
$$n \leq \frac{kx_0}{4f} \Rightarrow n=\frac{kx_0}{4f}+c$$
I need to show c=-1/4 to reach the given answer.

 

[gneill]

Okay, here's a way to think about it that should get you where you want to be

Each time a cycle completes the amplitude drops by a fixed amount 4f/k. So the displacement amplitude after n cycles is

$D = x_o - n \frac{4 f}{k}$

The force that the spring provides at displacement D is F = k*D. But the friction force f opposes motion, so we determine when the spring force becomes less than the frictional force (so the block can no longer move). The critical point is when F = f. (We're dealing with force magnitudes here, and not sweating the directions).

$f = F$
$f = k \left(x_o - n \frac{4 f}{k}\right)$

Solve for n.

 

[Saitama]

Okay, here's a way to think about it that should get you where you want to be

Each time a cycle completes the amplitude drops by a fixed amount 4f/k. So the displacement amplitude after n cycles is

$D = x_o - n \frac{4 f}{k}$

The force that the spring provides at displacement D is F = k*D. But the friction force f opposes motion, so we determine when the spring force becomes less than the frictional force (so the block can no longer move). The critical point is when F = f. (We're dealing with force magnitudes here, and not sweating the directions).

$f = F$
$f = k \left(x_o - n \frac{4 f}{k}\right)$

Solve for n.

Great, thanks a lot gneill!