6Stang7
- 212
- 0
As the title says, I have a statically indeterminate beam to the sixth degree and I'm attempting to use the superposition method (aka force method) to solve for the reactions. My additional equations will be the angle at points A, B, C, and D as well as the deflection at points B and C.
Is this the correct method to solve this, or is this the wrong approach? My thought is that this might not be right because the equations which are used to solve for the angle and deflection assume a linear differential equation, which I _think_ is not the case here.
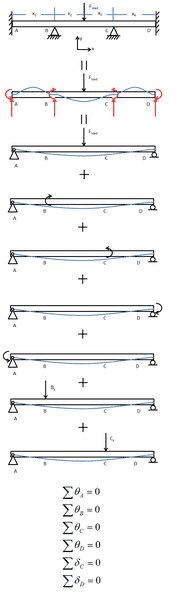
Is this the correct method to solve this, or is this the wrong approach? My thought is that this might not be right because the equations which are used to solve for the angle and deflection assume a linear differential equation, which I _think_ is not the case here.