SoylentBlue
- 50
- 8
Homework Statement
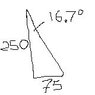
They ask for the smallest force P to apply if neither block is to slip. Coeff. of friction given as 0.25.
The 20KG block is 196N; the 10KG block is 98.1N
[/B]
Homework Equations
The Attempt at a Solution
[/B]
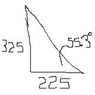
If we start at the 10KG block:
Sum of forces x: N + cos26.6P – (cos55.33)(N of 20KG block)
Sum of forces y: -98.1 –sin26.6P + 0.25N + (sin55.3)(N of 20KG block)
So, P pushes the 10KG block away from the wall, and N pushes the block away from the wall; and therefore we need a corresponding force in the x direction to pull it back toward the wall. That force must come from the 20KG block, which is a function of its normal force (multiplied by mu, which we know).
How do we find that?
Well, for the bigger block:
Sum of forces in y: -196.2 + N - (sin55.3)(98.1)-cos16.7P
We have to add in the downward pull of the smaller block (as a function of its geometry) here, right?
Stuck here. Too many variables: Two values of N (one for each block) plus P.
Any help would be appreciated. Thank you :^)