- #1
Dell
- 590
- 0
given the following points of the stress strain graph

and knowing that the stages are defined
linear σ=Eε
uniform plastic σ=Kδ2
necking σ=αδ
where ε is an elastic strain and δ plastic strain
find the values of the constants E K n α
using the given data i plotted σ(ε) and got the following
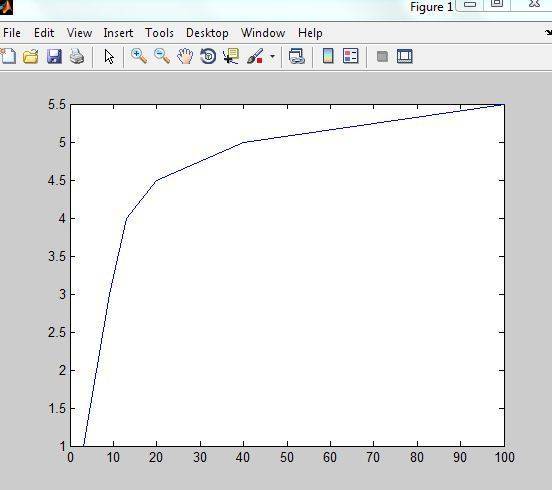
now to find the constant E, i take the linear portion and find its incline, i get
E=33.33MPa
as for the others
for the platic deformation, can i take an of the points after (3,9) ?
for each point i chose i get a different value
K=σ/δ2
K=4e4/(13e-4)2=2.366864e10
K=4.5e4/(20e-4)2=1.125e10
is the necking portion not meant to be after a maximum point in the graph? in this graph i have no such point.
and knowing that the stages are defined
linear σ=Eε
uniform plastic σ=Kδ2
necking σ=αδ
where ε is an elastic strain and δ plastic strain
find the values of the constants E K n α
using the given data i plotted σ(ε) and got the following
now to find the constant E, i take the linear portion and find its incline, i get
E=33.33MPa
as for the others
for the platic deformation, can i take an of the points after (3,9) ?
for each point i chose i get a different value
K=σ/δ2
K=4e4/(13e-4)2=2.366864e10
K=4.5e4/(20e-4)2=1.125e10
is the necking portion not meant to be after a maximum point in the graph? in this graph i have no such point.