Swinging in a conical pendulum

[charan1]

Homework Statement

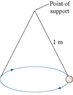
A conical pendulum is formed by attaching a 0.900 kg ball to a 1.00 m-long string, then allowing the mass to move in a horizontal circle of radius 10.0 cm. The figure (Intro 1 figure) shows that the string traces out the surface of a cone, hence the name. (Figure Attached)

What is the tension in the string? Got this one right 8.86N

What is the ball's angular velocity, in rpm? (Need help with this one)

Homework Equations

a=(w^2)(r)
Fnet=(m)(w^2)(r)

The Attempt at a Solution

I got the first question pretty easily, but then I did this to find the second and it was wrong, I think i did something wrong in my conversion from rad/s to rpm's please check.

I got the angle like this-
cos^-1=.05m/1m=87.13 degree's

Then for the Force towards the center of the circle on the x-plane-
cos(87.13) x 8.86N=.444N

Then for the angular velocity-

F=(w^2)(m)(r)
.444N=(w^2)(.9)(.1)

w=2.22 rad/s

Then convert to rpm-

2.22rad / 2pie x 60 seconds = 21.2rpm and this is wrong where did i go wrong?

 

[nasu]

I got the angle like this-
cos^-1=.05m/1m=87.13 degree's

If the radius is 10 cm (0.1 m) why do you have 0.05 here?
How did you get the tension without using the angle? With similar triangles?

 

[charan1]

Thanks I got it!

used the wrong r value to get the angle once I got the angle I calculated everything and got the answer to be 30 rpm