Frank-95
- 51
- 1
- TL;DR Summary
- I need to calculate the output pressure of a syringe pump driven by a stepper motor, given the step-rate of the motor itself, and the length of the tube connected to the syringe.
Hello.
I've built this syringe pump. The chosen motor is a NEMA 11 with a maximum torque of 6 Ncm.
The thread rod is an M5 with a pitch of 0.8 mm.
The whole system will consist also of a long tube (1 m length, 3.175 mm external diameter, 1.5875 internal diameter), at the end of which I'll need to place a spray nozzle which I have not bought yet.
I'm stuck at this point: given the syringe diameter, the tube length and diameter, the pitch of the thread, and the motor steprate, how do I calculate needed steprate to have a certain pressure?
The following image is taken from this thread, I didn't make it.
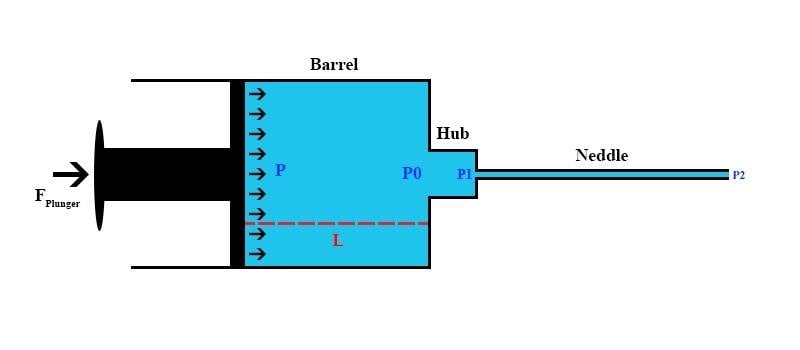
Last attempt was to use Hagen-Poiseuille formula for every section of the device. The long tube, the syringe tip and the syringe body.
So my P2 is the pressure I need (0,5 bar) plus atmospheric pressure, am I right? Then after I use that formula and I can say that losses along the syringe body are negligible so that P ≈ P0 ≈ P1. Now that I have calculated the necessary pressure at the plunger to obtain the needed output pressure and flow rate, which is the next step?
I thought of use these calculated pressures inside Bernoulli's principle, in order to get the linear velocity at the plunger and so calculating the steprate from that one, which is straightforward. Does it make any sense?
EDIT:
What I need is an output pressure of 0,5 bar and a flow rate of 233 μl/s
I've built this syringe pump. The chosen motor is a NEMA 11 with a maximum torque of 6 Ncm.
The thread rod is an M5 with a pitch of 0.8 mm.
The whole system will consist also of a long tube (1 m length, 3.175 mm external diameter, 1.5875 internal diameter), at the end of which I'll need to place a spray nozzle which I have not bought yet.
I'm stuck at this point: given the syringe diameter, the tube length and diameter, the pitch of the thread, and the motor steprate, how do I calculate needed steprate to have a certain pressure?
The following image is taken from this thread, I didn't make it.
Last attempt was to use Hagen-Poiseuille formula for every section of the device. The long tube, the syringe tip and the syringe body.
So my P2 is the pressure I need (0,5 bar) plus atmospheric pressure, am I right? Then after I use that formula and I can say that losses along the syringe body are negligible so that P ≈ P0 ≈ P1. Now that I have calculated the necessary pressure at the plunger to obtain the needed output pressure and flow rate, which is the next step?
I thought of use these calculated pressures inside Bernoulli's principle, in order to get the linear velocity at the plunger and so calculating the steprate from that one, which is straightforward. Does it make any sense?
EDIT:
What I need is an output pressure of 0,5 bar and a flow rate of 233 μl/s
Last edited: