ewiner
- 1
- 0
Homework Statement
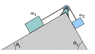
Figure 5-60 shows a box of dirty money (mass m1 = 2.7 kg) on a frictionless plane inclined at angle θ1 = 28°. The box is connected via a cord of negligible mass to a box of laundered money (mass m2 = 2.4 kg) on a frictionless plane inclined at angle θ2 = 64°. The pulley is frictionless and has negligible mass. What is the tension in the cord?
Homework Equations
F = ma
T - mgsin\Theta = -ma
a = ( m / M + m )g
The Attempt at a Solution
Newton's 2nd law for each body:
m1: T - (2.7 kg)(9.8 m/s2)sin28 = -(2.7 kg)a
m2: (2.4 kg)(9.8 m/s2)sin68 - T = -(2.4 kg)a
Add m1 & m2: (2.4 kg)(9.8 m/s2)sin68 - (2.7 kg)(9.8 m/s2)sin28 = (2.4 + 2.7)a
Solve for a: a = 1.84
Insert a into m1: T-(2.7 kg)(9.8 m/s2)sin28 = -(2.7 kg)(1.84 m/s2)
T = 17.4 N
However, that is not the right answer... Where am I going wrong?