beibixx
- 8
- 0
Let me know where my logic is off...Much thanks!
so
a)
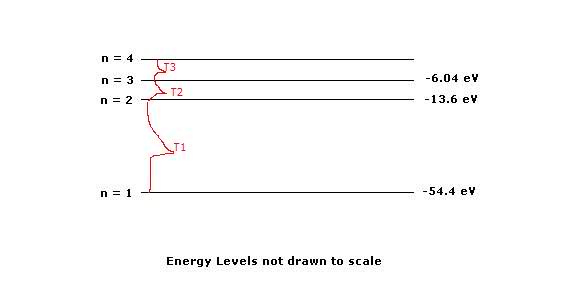
For T1: Transition -54.4-(-13.6) = 40.8 eV
For T2: -13.6 - (-6.04) = 7.56 eV
T3=?
n4 = n3
so
-6.04 + 7.56 = 1.52 eV
T3 = 1.52 eV
n4 = 1.52 eV
b)
E = pc
c = 6.63 x 10^-34 JS
p = E/c
p = 1.52/ 6.63 x 10^-34 JS
p=2.29 x 10^33
c)
KEmax = hf - wo
wo = hf , given wo = 4.7 eV
E = hf , given h = 4.14 x 10^-15 eV
f = E/h
f = (1.52)/(4.14 x 10^-15)
f = 3.67 x 10^14 Hz
KEmax = (4.14 x 10^-15) (3.67 x 10^14) - 4.7eV
KEmax = 1.519 - 4.7
KEmax = -3.18062 ... okay.. doesn't make sense?
so
a)
For T1: Transition -54.4-(-13.6) = 40.8 eV
For T2: -13.6 - (-6.04) = 7.56 eV
T3=?
n4 = n3
so
-6.04 + 7.56 = 1.52 eV
T3 = 1.52 eV
n4 = 1.52 eV
b)
E = pc
c = 6.63 x 10^-34 JS
p = E/c
p = 1.52/ 6.63 x 10^-34 JS
p=2.29 x 10^33
c)
KEmax = hf - wo
wo = hf , given wo = 4.7 eV
E = hf , given h = 4.14 x 10^-15 eV
f = E/h
f = (1.52)/(4.14 x 10^-15)
f = 3.67 x 10^14 Hz
KEmax = (4.14 x 10^-15) (3.67 x 10^14) - 4.7eV
KEmax = 1.519 - 4.7
KEmax = -3.18062 ... okay.. doesn't make sense?