The Tensor Algebra - Cooperstein, Example 10.1

[Math Amateur]

I am reading Bruce N. Coopersteins book: Advanced Linear Algebra (Second Edition) ... ...

I am focused on Section 10.3 The Tensor Algebra ... ...

I need help in order to get a basic understanding of Example 10.1 in Section 10.3 ...Example 10.1 plus some preliminary definitions reads as follows:

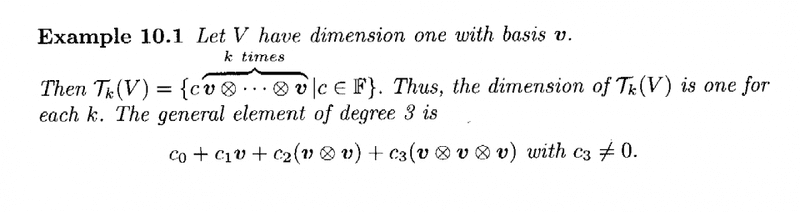
My questions related to Example 10.1 are articulated below ... ...
Question 1

In the above text from Cooperstein we read in Example 1, the following:" ... ... Then $\mathcal{T}_k (V) = \{ cv \otimes \ ... \ ... \ \otimes v \ | \ c \in \mathbb{F} \}$ ... ... "But ... $\mathcal{T}_k (V)$ is defined by

$\mathcal{T}_k (V) = V \otimes V \otimes V \ ... \ ... \ \otimes V$ ... ... ... (1)

( and there are $k$ $V$'s in the product ... )... surely then $\mathcal{T}_k (V) = \{ v \otimes \ ... \ ... \ \otimes v \ | \ v \in V \}$and not (as shown in Cooperstein Example 10.1 )

$\mathcal{T}_k (V) = \{ cv \otimes \ ... \ ... \ \otimes v \ | \ c \in \mathbb{F} \}$

... can someone please explain why $\mathcal{T}_k (V)$ has the form shown by Cooperstein in Example 10.1 ...Question 2

Can someone explain how/why the general element of degree 3 is as shown in Example 10.1 ...

Does it make sense to add these elements ... they seem different in nature and form ...Hope someone can help ...

Peter

 

[stevendaryl]

Question 1

In the above text from Cooperstein we read in Example 1, the following:" ... ... Then $\mathcal{T}_k (V) = \{ cv \otimes \ ... \ ... \ \otimes v \ | \ c \in \mathbb{F} \}$ ... ... "But ... $\mathcal{T}_k (V)$ is defined by

$\mathcal{T}_k (V) = V \otimes V \otimes V \ ... \ ... \ \otimes V$ ... ... ... (1)

( and there are $k$ $V$'s in the product ... )... surely then $\mathcal{T}_k (V) = \{ v \otimes \ ... \ ... \ \otimes v \ | \ v \in V \}$and not (as shown in Cooperstein Example 10.1 )

$\mathcal{T}_k (V) = \{ cv \otimes \ ... \ ... \ \otimes v \ | \ c \in \mathbb{F} \}$

... can someone please explain why $\mathcal{T}_k (V)$ has the form shown by Cooperstein in Example 10.1 ...

Since the $\mathcal{T}_k$ are vector spaces, a vector space is closed under multiplication by a constant. So if $v \otimes \ ... \ ... \ \otimes v$ is an element of the vector space, so is $c v \otimes \ ... \ ... \ \otimes v$

 

[andrewkirk]

Question 2
Can someone explain how/why the general element of degree 3 is as shown in Example 10.1 ...

Does it make sense to add these elements ... they seem different in nature and form ...

The key is where the author says 'We will often abuse notation and express $\boldsymbol x$ as a sum of its homogeneous parts rather than as a function from $\mathbb Z_{\geq 0}$'.

I note that this also explains the abuse of notation that caused you concern in your other post from yesterday. I have to retract my criticism of the author that I made there, as the excerpt you include here shows that he does explicitly acknowledge the abuse of notation. I beg your pardon, Mr Cooperstein.

The elements that are being added are functions from $\mathbb Z_{\geq 0}$ to $\bigcup_{k\in\mathbb Z_{\geq 0}}\mathcal T_k$. Because we have the constraint $\boldsymbol x(k)\in\mathcal T_k(V)$ and $\mathcal T_k(V)$ is a vector space (and hence has well-defined addition), we have the following natural definition of addition in $\mathcal T(V)$. For $\boldsymbol x,\boldsymbol y\in\mathcal T(V)$, $\boldsymbol x+\boldsymbol y$ is the function from $\mathbb Z_{\geq 0}$ to $\bigcup_{k\in\mathbb Z_{\geq 0}}\mathcal T_k$ such that, for all $k\in\mathbb Z_{\geq 0}$:
$$(\boldsymbol x+\boldsymbol y)(k)=\boldsymbol x(k)+\boldsymbol y(k)$$

 

[fresh_42]

Can someone explain how/why the general element of degree 3 is as shown in Example 10.1 ...

Does it make sense to add these elements ... they seem different in nature and form ...Hope someone can help ...

Peter

To get an idea of the tensors you can write vectors in coordinates, say $v = (v_1,...,v_n) , w = (w_1,...,w_n)$.
$\mathcal T_0 = \mathbb{F}, \mathcal T_1 = V$ and $\mathcal T_2$ can be seen as all $(n \times n)$ matrices.
An element $v\otimes w$ then is the rank $1$ matrix
$$v^τ \cdot w = \begin{bmatrix} v_1 \\ \vdots \\ v_n \end{bmatrix} \cdot (w_1, \cdots, w_n) = \begin{bmatrix} v_1w_1 &&\cdots && v_1w_n \\ \vdots && \cdots && \vdots \\ v_nw_1 && \cdots && v_nw_n\end{bmatrix} $$
and addition together with scalar multiplications of those matrices give you any $(n \times n)$ matrix you want.
The same procedure on $u\otimes v\otimes w$ will deliver a $(n \times n \times n)$ cube of rank $1$ and so on.

You are right that you cannot write the sum $c + v + v \otimes w + u \otimes v \otimes w$ other than this formal sum. However, in each component (the homogeneous parts of degree $0, 1, 2, 3,$ resp.) you can add and (scalar) multiply the elements as I mentioned in the case of rank $1$ matrices.

Another picture is that of a polynomial ring micromass mentioned elsewhere. If you have $ℝ[X,Y]$ you cannot add $X$ and $Y$ other than writing $X+Y$. Nevertheless this doesn't keep you from calculating with polynomials in two variables.

 

[Math Amateur]

Steven, Andrew and Fresh ... thank you for your helpful and clarifying posts ...

I am reflecting on what you have said ...

Thanks again,

Peter