- #1
erik-the-red
- 89
- 1
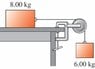
Consider the system shown in the figure. The rope and pulley have negligible mass, and the pulley is frictionless. The coefficient of kinetic friction between the 8.00-kg block and the tabletop is [tex]\mu_k=0.250.[/tex] The blocks are released from rest.
Use energy methods to calculate the speed of the 6.00-kg block after it has descended 1.50 m.
[tex]\Delta * K[/tex] = [tex](1/2)(m)(v_f^2 - v_i^2)[/tex]
But, it was at rest, so [tex](1/2)(m)(v_f^2)[/tex] is what matters.
What do I do next?
Use energy methods to calculate the speed of the 6.00-kg block after it has descended 1.50 m.
[tex]\Delta * K[/tex] = [tex](1/2)(m)(v_f^2 - v_i^2)[/tex]
But, it was at rest, so [tex](1/2)(m)(v_f^2)[/tex] is what matters.
What do I do next?
