Ambforc
- 14
- 0
Here is a second thought experiment I designed to test if I understand certain concepts concerning electrostatics correctly. Help will be appreciated.
There must be an error somewhere in the explanation below; I am giving the explanation as if “factual” only to explain how I understand it at present.
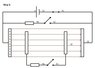
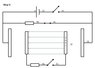
Consider the setup shown in the figure for step 1. The potential difference source (cell V1) charged capacitor C1 to full capacity (voltage over capacitor equal to voltage over cell).
In step 2 switch S1 is opened, and S3 is connected next. Work is done on resistor R2 as charges separate between the plates to establish an opposing electric field so that the potential difference between the two conductive plates of capacitor C2 is zero.
Step 3 involves opening switch S3 and closing switch S2 afterwards. Work is done on resistor R1 as the current flows to equalize the charges on the plates of capacitor C1.
Step 4 is to close switch S3. Work will again be done on resistor R2 as the current flows to equalize the charges on the plates. Get back to step 1 by opening switch S3 and S2, and closing switch S1. The cell will do work to charge capacitor C1.
Assuming that there is no dielectric effect on capacitor C1 due to the charged plates of C2 in the middle of it (cannot see why there should be as the electric field due to the charged plates C2 is supposed to be zero to the left and right of capacitor C2), the work done in step 3 is equal to the work done on the cell to recharge capacitor C1 (assuming a fully efficient, reversible charging and discharging process on the capacitor). This leaves the work done on resistor R2 in steps 2 and 4 as excess from the cycle, something that is not supposed to happen.
I will appreciate a pointer as to what I overlook.
There must be an error somewhere in the explanation below; I am giving the explanation as if “factual” only to explain how I understand it at present.
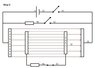
Consider the setup shown in the figure for step 1. The potential difference source (cell V1) charged capacitor C1 to full capacity (voltage over capacitor equal to voltage over cell).
In step 2 switch S1 is opened, and S3 is connected next. Work is done on resistor R2 as charges separate between the plates to establish an opposing electric field so that the potential difference between the two conductive plates of capacitor C2 is zero.
Step 3 involves opening switch S3 and closing switch S2 afterwards. Work is done on resistor R1 as the current flows to equalize the charges on the plates of capacitor C1.
Step 4 is to close switch S3. Work will again be done on resistor R2 as the current flows to equalize the charges on the plates. Get back to step 1 by opening switch S3 and S2, and closing switch S1. The cell will do work to charge capacitor C1.
Assuming that there is no dielectric effect on capacitor C1 due to the charged plates of C2 in the middle of it (cannot see why there should be as the electric field due to the charged plates C2 is supposed to be zero to the left and right of capacitor C2), the work done in step 3 is equal to the work done on the cell to recharge capacitor C1 (assuming a fully efficient, reversible charging and discharging process on the capacitor). This leaves the work done on resistor R2 in steps 2 and 4 as excess from the cycle, something that is not supposed to happen.
I will appreciate a pointer as to what I overlook.
Attachments
Last edited: