- #1
phantomvommand
- 272
- 39
- Homework Statement
- Please refer to the picture below.
- Relevant Equations
- pV = nRT
Knowledge of vaporisation, condensation, and the 4 thermal processes.
It is a long problem, but it is simple to understand.

I am having trouble with part A. My attempt:
Pressure outside > pressure inside container. pV = constant (isothermal). At equilibrium, all gases are at atmospheric pressure. Because it is quasi-static, the pressures of both compartments are equal at all times, implying that their volumes are equal at all times as well, as pV = const. This means that at equilibrium with the atmosphere, the volume of each compartment is 0.5V0.
However, the answer writes that after equilibrium with the atmosphere is attained, all the water vapour condenses, and throughout this condensation, pressure somehow remains at 1 atm, only that volume of the left chamber decreases to 0. Why would condensation even occur, and if it does how does the pressure remain at 1 atm while the volume goes to 0?
Furthermore, after the complete condensation of water vapour, the N2 gas in the right chamber undergoes yet another isothermal compression, such that its pressure is now 2 atm, despite the outside pressure being only 1 atm. How is this possible?
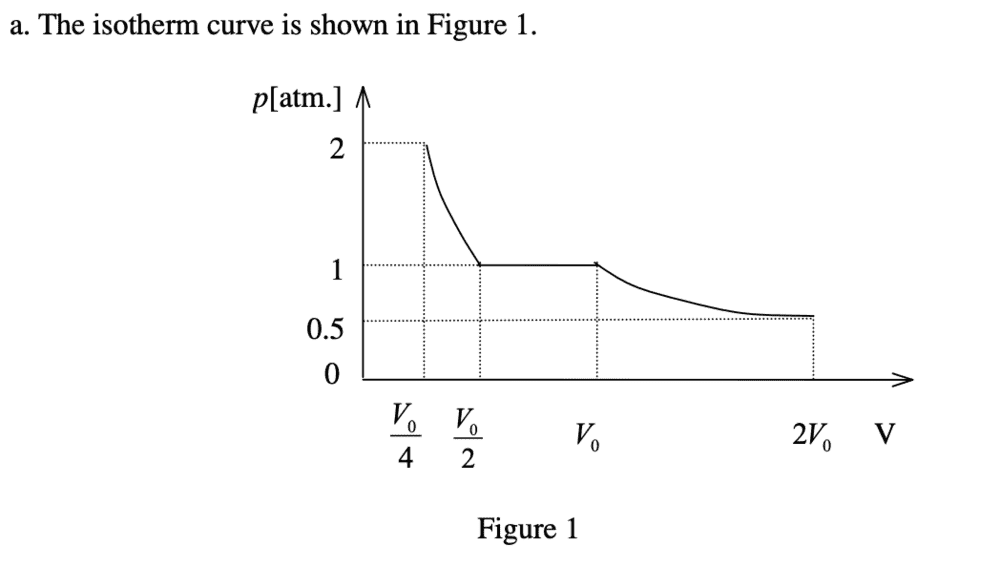
I am having trouble with part A. My attempt:
Pressure outside > pressure inside container. pV = constant (isothermal). At equilibrium, all gases are at atmospheric pressure. Because it is quasi-static, the pressures of both compartments are equal at all times, implying that their volumes are equal at all times as well, as pV = const. This means that at equilibrium with the atmosphere, the volume of each compartment is 0.5V0.
However, the answer writes that after equilibrium with the atmosphere is attained, all the water vapour condenses, and throughout this condensation, pressure somehow remains at 1 atm, only that volume of the left chamber decreases to 0. Why would condensation even occur, and if it does how does the pressure remain at 1 atm while the volume goes to 0?
Furthermore, after the complete condensation of water vapour, the N2 gas in the right chamber undergoes yet another isothermal compression, such that its pressure is now 2 atm, despite the outside pressure being only 1 atm. How is this possible?