physiks
- 101
- 0
Homework Statement
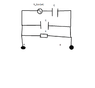
I have the network attached below. I need to find the open circuit voltage and short circuit current between A and B and then use these to find the Thevenin equivalent for the circuit.
The Thevenin equivalent voltage is of the form VTsinwt and the equivalent impedance is ZT.
Homework Equations
I know the Thevenin voltage is just the open circuit voltage between A and B, and the Thevenin impedance is the Thevenin voltage over the short circuit current. The only issue is of course finding these.
The Attempt at a Solution
My idea is to reduce the series RC combination into a single impedance, and then find the total current. Then the open circuit voltage is that of the voltage source minus the voltage drop across the capacitor. The voltage drop across the capacitor is the total current times the capacitor impedance.
However this turns out to be very messy, so I'm not sure if it's right or if there is a better way.
Also for the short circuit current, would that just be the current the flows in a circuit that contained the voltage source in series with C, as no current goes down the resistor path or of the other capacitor.