Marshillboy
- 21
- 0
Homework Statement
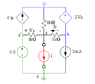
See attached image
Homework Equations
Thevenin's theorem
Node voltage method?
The Attempt at a Solution
So if I want the current Io, I believe I need to treat the 1K resistor as an open circuit in finding the Thevenin equivalent. I think setting ground to be the bottom node is a good idea.
One trick I'm familiar with to find the Thevenin equivalent resistance is to replace the current sources with open circuits and the voltage sources with short circuits and find the resistance between the two points. I think this gives me just 1kOhm between "a" and "b"(ground) for my Thevenin resistance. Does this only work with independent sources?
I'm not sure how to find the Thevenin voltage. All these dependent sources are psyching me out. I've tried to use the node voltage method, treating the top right dependent source as a supernode, but I'm pretty sure I got a wrong answer from that, since my system of equations tells me there is an independent variable (which shouldn't happen when solving these equations simultaneously).
Attachments
Last edited: