Time period of a pendulum made of two disks

[vishwesh]

Homework Statement

Problem statement -
[/B]
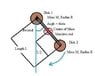
Klepner and Kolenkow 6.15 : A pendulum is made of two disks each of mass M and radius R separated by a massless rod. One of the disks is pivoted through its center by a small pin. The disks hang in the same plane and their centres are a distance l apart. Find the period for small oscillations.

Variables -

Two disks of mass M and radius R; massless rod; distance between centres of disks is l

Homework Equations

For disk, radius of gyration, k = $\sqrt{\cfrac{1}{2}}R$
For a physical pendulum,

$\omega = \sqrt{\cfrac{mgl}{I}}$, where m = mass of the physical pendulum and I = moment of inertia of the pendulum about the pivot.

The Attempt at a Solution

[/B]
Centre of mass of the system of the disks should be at the midpoint of the rod. So, I replaced the system with a physical pendulum.

First, we have to calculate moment of inertia of the pendulum about the pivot. Using parallel axis theorem,

$I = I_{0} + ml^2$
$\implies I = \cfrac{1}{2}(2M)R^2 + (2M) (\cfrac{l}{2})^2$

Also, we will have to replace 'm' by '2M' in the formula for $\omega$.

This whole solution of mine looks too confusing to me. Can anyone please tell me whether I am on the right path or not? Also, how should I proceed with the question?

I have attached the figure for the question (as per my understanding).

Thanks

 

[Simon Bridge]

You have the right basic approach - you need the moment of inertia about the pivot - which is actually through the center of mass of one of the disks. The overall moment of inertia is the sum of the moments of inertia of the parts. So work out each part separately and add them up.

 

[vishwesh]

You have the right basic approach - you need the moment of inertia about the pivot - which is actually through the center of mass of one of the disks. The overall moment of inertia is the sum of the moments of inertia of the parts. So work out each part separately and add them up.

Thanks for the reply.

Net moment of inertia, $I_{net} = I_{1} + I_{2} = \cfrac{1}{2} MR^2 + (\cfrac{1}{2}MR^2 + Ml^2)$
$\implies I_{net} = MR^2 + Ml^2$

Plugging in the values in the formula:

$\omega = \sqrt{\cfrac{mgl}{I}} = \sqrt{\cfrac{(2M)g(\cfrac{l}{2})}{MR^2 + Ml^2}}$
$\implies \omega = \sqrt{\cfrac{gl}{R^2 + l^2}}$

Thus, time period of oscillations should be:

$T = \cfrac{2\pi}{\omega} = 2\pi \sqrt{\cfrac{R^2 + l^2}{gl}}$

Is this correct?

Thanks

 

[Simon Bridge]

It's pretty much what I would have done - didn't check your algebra.

 

[vishwesh]

It's pretty much what I would have done - didn't check your algebra.

Superb! Thanks a lot for your help.