sid0123
- 48
- 5
Homework Statement
In an infinite flat layer of thickness 2d, volume charge density is given according to the law: ρ=(ρ°)(x)/d and (-d≤x≤d). Here, x is the axis perpendicular to the plane. In the layer, there is a thin channel in which a point dipole of mass m and dipole moment p is placed. Calculate the time period of small oscillations of the dipole.
Homework Equations
Differential form of electric field:
div E = 4πρ and
div E = ∂Ex/∂x + ∂Ey/∂y + ∂Ez/∂z
The Attempt at a Solution
"Attempt to the solution has been made in CGS system"
div E = 4πρ
∂Ex/∂x + ∂Ey/∂y + ∂Ez/∂z = 4πρ
∂Ey/∂y and ∂Ez/∂z will be zero.
Therefore,
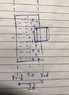
∂Ex/∂x = 4πρ =(4πρ°x)/d
Ex(x) = (4πρ°)/d ∫x dx = [(4πρ°)/d]*[x2]/2 = (2πρ°x2)/d + C
How will we find the constant C?
What exactly will be the electric field at point d from the midpoint of the layer? Will it be 2πρ°(2d) = 4πρ°d?
I am confused how to proceed from here.
Last edited: