Time period of small oscillations of the point dipole

AI Thread Summary
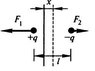
The discussion revolves around calculating the time period of small oscillations of a point dipole placed in an infinite flat layer with a specified volume charge density. Participants analyze the electric field generated by the charge distribution, using the divergence of the electric field and integrating to find expressions for E(x). There is confusion regarding the constants involved and the conditions at specific points, particularly at x=0, where the electric field is debated to be non-zero due to the surrounding charge distribution. The final expression for the time period of oscillation is proposed as √[(πmd)/(ρ°p)], although the necessity of the dipole's charge separation distance remains a point of contention. The conversation highlights the complexities of applying different unit systems, such as CGS and SI, in solving the problem.
  • #51
@sid0123, when you have derived the E field to your satisfaction, look at post #49!
(Using gaussian cylinder method is still applicable).
 
Physics news on Phys.org
  • #52
Thank you very much, everyone. I understood it but took a little time to reply back. And yes, they were linear oscillations.
 
  • #53
Thank you, everyone for making me understand this. Sorry for taking a little long to reply. And yes, they were linear oscillations
 

Similar threads

Torque acting on dipole
Replies
28
Views
997
Effect of different magnetic fields on a magnetic dipole
Replies
25
Views
1K
A charge inside a ring, small oscillation
Replies
2
Views
1K
Time Period of a Small Oscillation
Replies
26
Views
5K
Electric field created by point charges
Replies
6
Views
747
Determine the period of small oscillations
Replies
11
Views
3K
Electric field of point along the central vertical axis of a triangle
Replies
3
Views
796
Electric Field Line Homework: Deriving Analytical Expressions
Replies
1
Views
2K
What is the Potential Difference in a Non-Uniform Electric Field?
Replies
3
Views
2K
Time dependant Potential Energy in ion trap
Replies
1
Views
1K

Hot Threads

Recent Insights

Back
Top