vtech
- 12
- 0
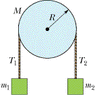
Wer are given two objects of mass m1 = .20 kg and m2 = .67 kg, which are connected by a massless cord that is wrapped around a uniform disk of mass M = 0.50 kg and radius R = 0.12 m. The disk can rotate without friction about a fixed horizontal axis through its center; the cord cannot slip on the disk. The system is released from rest.
(a) Find the magnitude of the acceleration of the blocks____m/s2
(b) Find the tension T1 in the cord at the left____ N
(c) Find the tension T2 in the cord at the right____N
--------------------------------------------------------------------------
well so far i have three equations - clockwise motion
1) T2*R - T1*R = I*alpha = net torque where alpha = a/R for pulley
2) T2 - m2*g = m2*a for mass on pulley
3) -T1 + m1*g = m1*a for mass on pulley
Then I solve 2) and 3) for respective tensions T2, T1 and substitute into 1) and solve for "a" I mean, am I close here or no? Cuz I don't want to write all of my solving out if I'm at the wrong starting point anyway...kinda messy... but I'm getting an answer of
a = - 7.429m/s2 but I get it as wrong. Don't have actual answer. Negative? So I'm guessing goes in opposite direction...?
Without correct a can't solve for T1 & T2 ... for answer a) since magnitude is being asked, even if acceleration is negative answer is +ve value.
I'd really appreciate some input on this questions! Thanks in advance!
(a) Find the magnitude of the acceleration of the blocks____m/s2
(b) Find the tension T1 in the cord at the left____ N
(c) Find the tension T2 in the cord at the right____N
--------------------------------------------------------------------------
well so far i have three equations - clockwise motion
1) T2*R - T1*R = I*alpha = net torque where alpha = a/R for pulley
2) T2 - m2*g = m2*a for mass on pulley
3) -T1 + m1*g = m1*a for mass on pulley
Then I solve 2) and 3) for respective tensions T2, T1 and substitute into 1) and solve for "a" I mean, am I close here or no? Cuz I don't want to write all of my solving out if I'm at the wrong starting point anyway...kinda messy... but I'm getting an answer of
a = - 7.429m/s2 but I get it as wrong. Don't have actual answer. Negative? So I'm guessing goes in opposite direction...?
Without correct a can't solve for T1 & T2 ... for answer a) since magnitude is being asked, even if acceleration is negative answer is +ve value.
I'd really appreciate some input on this questions! Thanks in advance!