Torque calculation of CV joint

[Gozupa]

TL;DR Summary: help with assignment: find CV joint torque in 3 different situations

Hi, I need help for my assignment. I need to calculate torque of CV joint of truck in 3 cases:
a) CV joint torque on take off
b) CV joint torque on take off on a slope in reverse
c) CV joint torque while driving on straight asphalt road

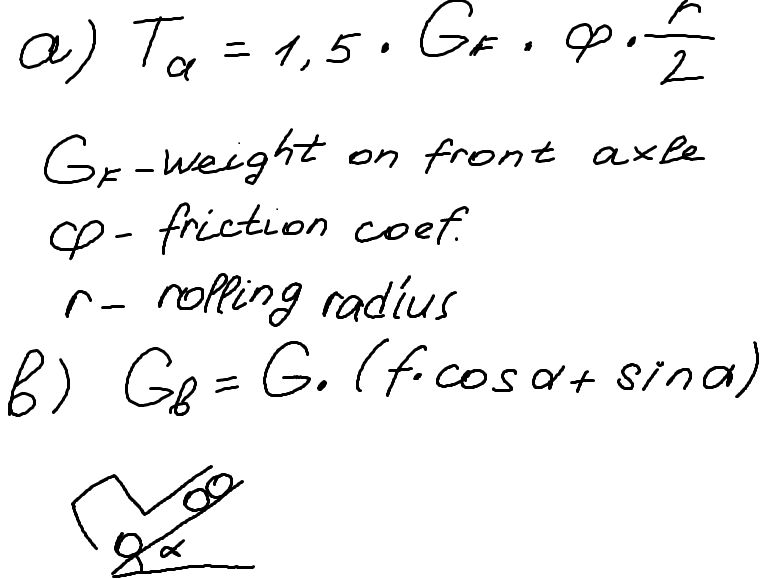
i've found formula (a) in one of my textbooks, but i'm not sure it's correct one. I don't know how to calculate (b) or (c) tbh.

 

[Lnewqban]

Welcome, @Gozupa !

It is impossible to help you with such limited information.
Are you asked to compare torque values or to calculate them?

CV joints are mainly used in front-wheel drive light vehicles.
Is your truck of that type?

That is important to know in order to properly answer the questions because the maximum possible force of friction between the tires and the asphalt determines the maximum torque that the engine's power can transfer to the wheels via the CV joints.

Once one wheel reaches that limit and starts spinning in place, the transmitted torque on the CV joint is greatly reduced due to lack of resistance from the asphalt.

For each case:
a) On take off: There is more weight (or normal force associated to friction) on the rear wheels than on the front ones.
b) On take off on a slope in reverse: There is more weight (or normal force associated to friction) on the front wheels than on the rear ones.
c) On straight asphalt road: There is about the same weight (or normal force associated to friction) on the rear wheels and on the front ones.

 

[haruspex]

c) On straight asphalt road: There is about the same weight (or normal force associated to friction) on the rear wheels and on the front ones.

At constant speed, that is.